手撕卡尔曼滤波器

卡尔曼滤波器（Kalman Filter），从字面意思上来看，“Filter滤波器”一词并不能很好地体现其特性。卡尔曼滤波器用一句话来说就是“Optimal Recursive Data-Processing Algorithm”，即为“最优化递归数字处理算法”，它更像是一种观测器，而不是一般意义上的滤波器。卡尔曼滤波器的应用非常广泛，尤其是在导航中。它的广泛应用是因为世界中存在大量的不确定性，当我们描述一个系统时，这个不确定性主要体现在三个方面：

不存在完美的数学模型
系统的扰动不可控，也很难建模
测量传感器存在误差

递归算法

下面看一个例子，多次用同一把尺子测量同一枚硬币的直径，用 $z_k$ 表示第k次的测量结果。由于种种误差，测量得到：

$\begin{aligned} z_1=50.1mm \\ z_2=50.4mm \\ z_3=50.2mm \end{aligned}$

此时如果要估计真实结果，自然而然地会想到取平均值。用 $\hat{x}_k$ 表示第k次的估计值，可以得到：

$\begin{aligned} \hat{x}_k &= \frac{1}{k}(z_1+z_2+\cdots+z_k)\\ &= \frac{1}{k}(z_1+z_2+\cdots+z_{k-1}) + \frac{1}{k}(z_k)\\ &= \frac{k-1}{k}\frac{1}{k-1}(z_1+z_2+\cdots+z_{k-1}) + \frac{1}{k}(z_k)\\ &= \frac{k-1}{k}\hat{x}_{k-1} + \frac{1}{k}(z_k)\\ &= \hat{x}_{k-1} + \frac{1}{k}(z_k-\hat{x}_{k-1}) \end{aligned}$

上式中，第三行 $\frac{1}{k-1}(z_1+z_2+\cdots+z_{k-1})$ 就是 $k-1$ 次的平均值 $\hat{x}_{k-1}$

观察最后一行结论，$k\uparrow, \frac{1}{k-1}\to0,\hat{x}_k\to\hat{x}_{k-1}$ ，也就是说，随着k的增加，此时拥有了大量的数据，对估计的结果就比较有信心了，测量的结果就不是很重要了。相反，如果k比较小， $\frac{1}{k-1}$ 就会比较大，测量结果 $z_k$ 就会起到很大的作用，尤其是测量结果和估计值差距比较大的时候。

令 $K_k=\frac{1}{k-1}$ ，则此时公式可以表示为：

$\hat{x}_k = \hat{x}_{k-1} + K_k(z_k-\hat{x}_{k-1})$

上式表示的含义为：当前的估计值 = 上一次的估计值 + 系数 * ( 当前测量值 - 上一次的估计值 ) ，其中的 $K_k$ 就是卡尔曼增益/因数（Kalman Gain），通过这个公式可以看出，新的估计值 $\hat{x}_k$ 与上一次的估计值 $\hat{x}_{k-1}$ 有关，上一次的又与上上次的有关，这就是一种递归思想（Recursive），这也是卡尔曼滤波器的优势，他不需要追溯很久以前的数据，只需要上一次的就可以。下面来讨论一下这个 $K_k$ ：

引入两个误差：

估计误差 $e_{EST}$ （e代表误差error，EST代表估计estimate）
测量误差 $e_{MEA}$ （e代表误差error，MEA代表测量measurement）

则 $K_k$ 可以表示为

$K_k = \frac{e_{EST_{k-1}}}{e_{EST_{k-1}}+e_{MEA_{k}}}$

这个公式是卡尔曼滤波中的核心公式，具体的推导后文会讲到。下面对这个公式进行讨论。在k时刻，

当 $e_{EST_{k-1}} \gg e_{MEA_{k}}$ ， $K_k\rightarrow1$ ，此时 $\hat{x}_k = z_k$ ，这说明当第k-1次的估计误差远大于第k次的测量误差时，第k次的估计值很趋近于测量值。（估计的误差大，测量的误差小，更信任测量值）
当 $e_{EST_{k-1}} \ll e_{MEA_{k}}$ ， $K_k\rightarrow 0$ ，此时 $\hat{x}_k = \hat{x}_{k-1}$ ，这说明当第k-1次的估计误差远小于第k次的测量误差时，第k次的估计值很趋近于测量值。（估计的误差小，测量的误差大，更信任估计值）

运用以上知识，解决一个实际问题可以分为三步：

计算卡尔曼增益 $K_k$ ，公式见前文
计算估算值 $\hat{x}_k$ ，公式见前文
更新估计误差 $e_{EST_{k}} = (1-K_k)e_{EST_{k-1}}$ ，此公式推导见后文。

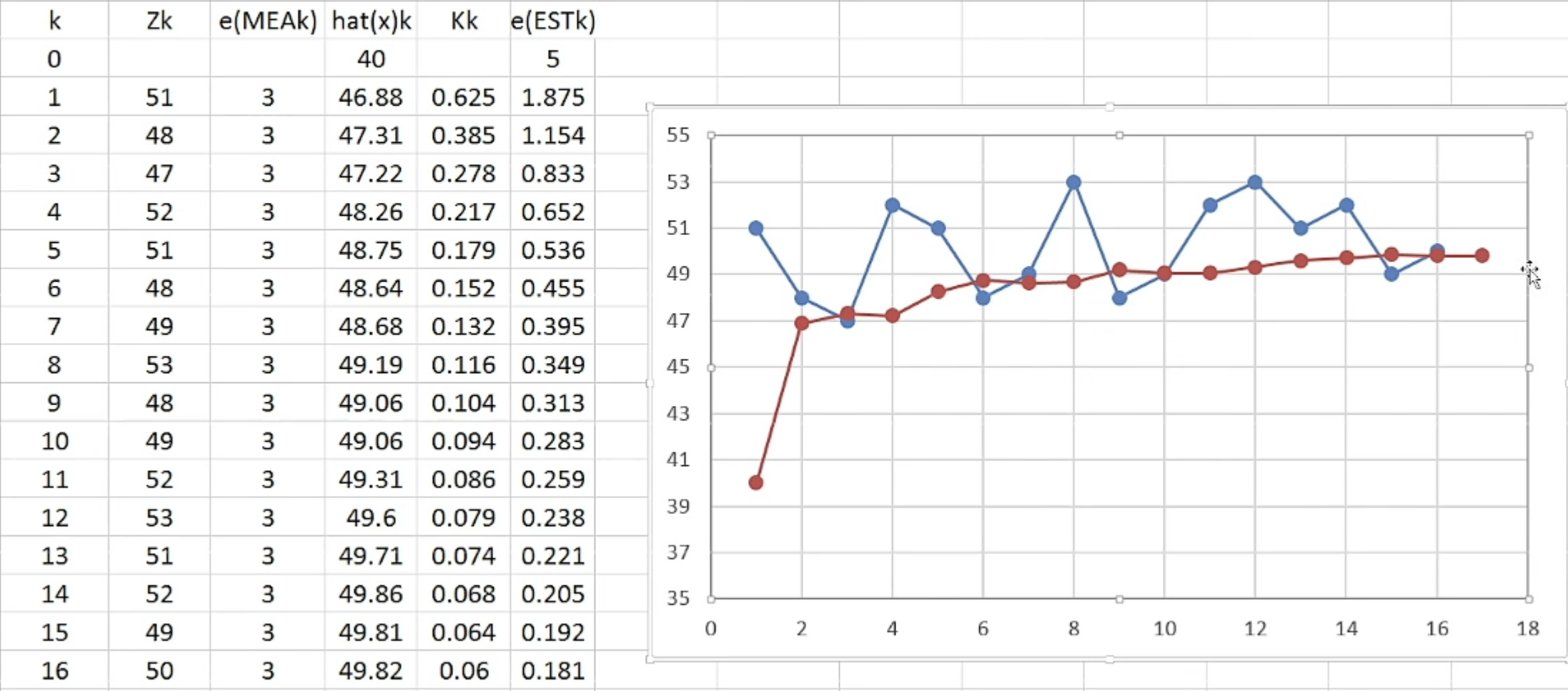
再看前文测量硬币直径的例子，实际长度 $x=50mm$ ，对于第一次测量：

$\begin{aligned} \hat{x}_0=40mm \\ e_{EST_{0}}=5mm \\ z_1=51mm\\ e_{MEA_{k}}=3mm \end{aligned}$

估计值是是随便估计的一个值；估计误差随便给一个数；测量值是实际测量得到的；由于测量工具不变，测量误差是一个恒定值。接下来进行递归：

蓝色是测量值 $z_k$ ，红色为估计值 $\hat{x}_k$ ，可以看到经过反复迭代，估计值越来越接近实际值。这就是卡尔曼滤波器的递归思想。

数学基础

数据融合

下面举例说明数据融合（Data Fusion）

分别用两个称称一个东西，得到两个结果，分别为

$\begin{aligned} z_1=30mm \\ z_2=32mm \end{aligned}$

两个称都有误差，两个称的标准差（Standard Deviation）分别为：

$\begin{aligned} \sigma_1=2g \\ \sigma_2=4g \end{aligned}$

他们均符合正态分布/高斯分布（Natural/Gaussin Distribution）

如果用这两个结果去估计真实值 $\hat{z}=?$ ，可以用到上一节的思想，则

$\begin{array}{c} \hat{z} = z_{1} + K(z_2-z_{1}),k\in[0,1] \\ k=0,\hat{z}=z_1\\ k=1,\hat{z}=z_2 \end{array}$

求k使得 $\sigma_{\hat{z}}$ 最小，也就是使得方差 $Var(\hat{z})$ 最小

$\begin{aligned} \sigma_{\hat{z}}^2&=Var(\hat{z})\\ &=Var(z_1 + K(z_2-z_1))\\ &=Var(z_1 -Kz_1+ Kz_2)\\ &=Var((1-K)z_1+ Kz_2)\\ &=Var((1-K)z_1)+Var(Kz_2)\\ &=(1-K)^2Var(z_1)+K^2Var(z_2)\\ &=(1-K)^2\sigma_1^2+K^2\sigma_2^2\\ \end{aligned}$

可以看到，第四行中 $(1-K)z_1$ 和 $Kz_2$ 是互相独立的，因为两个称的结果不会互相影响，所以由于方差的性质可以写成两个独立的方差。要求这个式子的最小值，就要对K求导并令导数等于0。可以解出K：

$\begin{array}{c} \frac{d\sigma_{\hat{z}}^2}{dK}=0\\ -2(1-K)\sigma_1^2+2K\sigma_2^2=0\\ K=\frac{\sigma_1^2}{\sigma_1^2+\sigma_2^2}=\frac{2^2}{2^2+4^2}=0.2 \end{array}$

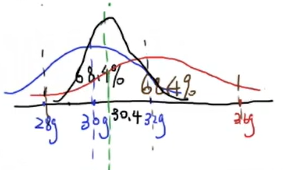
将K带入上面的式子，得到 $\hat{z}=30.4$ 。此时为最优解。计算此时的标准差 $\sigma_{\hat{z}}=1.79$ ，绘出正态分布图：

得到比两个图形更高更瘦的图形，这个过程就叫数据融合。

协方差矩阵

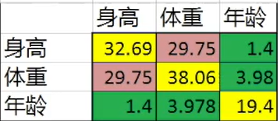
协方差矩阵（Covarince Matrix）是把方差和协方差在一个矩阵中表示出来，体现了变量间的联动关系。下面举例说明：

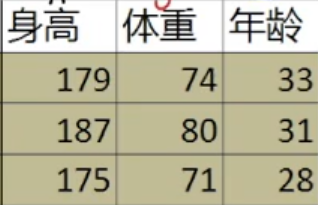
令身高为x，体重为y，年龄为z，分别计算平均值，方差和协方差（拿x举例）：

$\begin{aligned} \sigma_x^2&=\frac{1}{3}((179-180.3)^2\\ &\qquad+(187-180.3)^2\\ &\qquad+(175-180.3)^2)\\ &=24.89\\ \sigma_x\sigma_y&=\frac{1}{3}((179-180.3)(74-75)\\ &\qquad+(187-180.3)(80-75)\\ &\qquad+(175-180.3)(71-75))\\ &=18.7=\sigma_y\sigma_x \end{aligned}$

观察协方差的每一项，如果两个括号内都为负数，相乘为正数；两个括号内都为正数，相乘仍为正数；但一正一负相乘得到负数。所以最后加在一起的结果如果是正数，说明这两个变量的变化方向是一样的；如果是负数，说明这两个变量的变化方向是相反的。

协方差矩阵表示形式为：

$P = \begin{bmatrix} \sigma_x^2 & \sigma_x\sigma_y & \sigma_x\sigma_z \\ \sigma_y\sigma_x & \sigma_y^2 & \sigma_y\sigma_z \\ \sigma_z\sigma_x & \sigma_z\sigma_y & \sigma_z^2 \end{bmatrix}$

如果需要编程实现，可以通过以下方法求得P（其中a为过渡矩阵）

$\begin{aligned} a & = \begin{bmatrix} x_1 & y_1 & z_1 \\ x_2 & y_2 & z_2 \\ x_3 & y_3 & z_3 \end{bmatrix}-\frac{1}{3} \begin{bmatrix} 1 & 1 & 1 \\ 1 & 1 & 1 \\ 1 & 1 & 1 \end{bmatrix} \begin{bmatrix} x_1 & y_1 & z_1 \\ x_2 & y_2 & z_2 \\ x_3 & y_3 & z_3 \end{bmatrix}\\ P & = \frac{1}{3}a^Ta \end{aligned}$

多取一些数据，得到协方差矩阵，可以利用协方差矩阵分析各个数据之间的关系；

从协方差矩阵中可以看到，对角线上的数为方差，这些数据比较大，说明了这些变量之间跨度比较大。剩下的数据为协方差，体重和身高的协方差比较大，说明他们是正相关的，身高增加体重也增加；而年龄和其余两者的协方差比较小，说明他们之间的相关性比较小。

状态空间方程

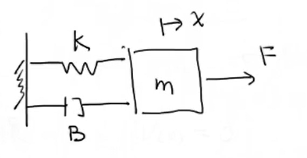
状态空间表达（State Space Representation），现代控制理论就是以状态空间方程为基础的。以弹簧振动阻尼系统为例：

动态方程表达式为：

$m\ddot{x}+B\dot{x}+kx=F$

将F定义为u，也就是系统的输入（Input）。将其转化成状态空间表达形式，定义两个状态（State）变量 $x_1=x$ ， $x_2=\dot{x}$ ，则

$\begin{aligned} \dot{x_1}&=x_2\\ \dot{x_2}&=\ddot{x}\\ &=\frac{1}{m}u-\frac{B}{m}\dot{x}-\frac{k}{m}x\\ &=\frac{1}{m}u-\frac{B}{m}x_2-\frac{k}{m}x_1 \end{aligned}$

这样就用两个一阶微分方程表达出来了。定义两个测量（Meansurement）变量，位置 $z_1=x=x_1$ ，速度 $z_2=\dot{x}=x_2$

将上面的式子改写成矩阵形式：

$\begin{aligned} \begin{bmatrix} \dot{x_1} \\ \dot{x_2} \end{bmatrix} & = \begin{bmatrix} 0 & 1 \\ -\frac{k}{m} & -\frac{B}{m} \end{bmatrix} \begin{bmatrix} x_1 \\ x_2 \end{bmatrix}+ \begin{bmatrix} 0 \\ \frac{1}{m} \end{bmatrix}u\\ \begin{bmatrix} z_1 \\ z_2 \end{bmatrix} & = \begin{bmatrix} 1 & 0 \\ 0 & 1 \end{bmatrix} \begin{bmatrix} x_1 \\ x_2 \end{bmatrix} \end{aligned}$

归纳出状态空间的表达形式：

$\begin{array}{l} \dot{x}(t)=Ax(t)+Bu(t)\\ z(t)=Hx(t) \end{array}$

这是一种连续的表达形式， $\dot{x}(t)$ 为x对时间的导数，体现了x随时间的变化。

如果写成离散形式(本节不深入讲解离散型，只做了解)，其中下标 $k-1,k,k+1$ 里面的1代表一个时间单位，即为采样时间（Sample Time），这种形式体现了上一步到这一步的一种变化：

$\begin{array}{l} x_k=Ax_{k-1}+Bu_{k-1}\\ z_k=Hx_k \end{array}$

如果增加一些开头提到的不确定性，其中 $w_{k-1}$ 为过程噪音（Process Noise）， $v_k$ 为测量噪音（Meansurement Noise）：

$\begin{array}{l} x_k=Ax_{k-1}+Bu_{k-1}+w_{k-1}\\ z_k=Hx_k+v_k \end{array}$

也就是说当估计结果 $x_k$ 不准确，测量结果 $z_k$ 也不准确的情况下，如何估计一个精确的 $\hat{x}_k$ ？这就是卡尔曼滤波器所要解决的问题。

卡尔曼增益数学推导

在上文的状态空间方程中， $x_k$ 为状态变量，A为状态矩阵，B为控制矩阵， $u_k$ 为控制， $w_{k-1}$ 为过程噪音， $v_k$ 为测量噪音，其中噪声是不可测的，是系统不确定性的表现。但过程噪声可以假设其符合正态分布 $P(w)\sim N(0,Q)$ ，其中0为期望，Q为协方差矩阵：

$\begin{aligned} Q&=E(ww^T)\\ &=E\left( \begin{bmatrix} w_1 \\ w_2 \end{bmatrix} \begin{bmatrix} w_1 & w_2 \end{bmatrix} \right)\\ &=E\left( \begin{bmatrix} w_1^2 & w_1w_2\\ w_2w_1 & w_2^2 \end{bmatrix} \right)\\ &= \begin{bmatrix} E(w_1^2) & E(w_1w_2)\\ E(w_2w_1) & E(w_2^2) \end{bmatrix}\\ &= \begin{bmatrix} \sigma_{w_1}^2 & \sigma_{w_1}\sigma_{w_2} \\ \sigma_{w_2}\sigma_{w_1} & \sigma_{w_2}^2 \end{bmatrix} \end{aligned}$

通过Q这个协方差矩阵可以表示出过程噪声的方差，亦可以表示出过程噪声之间的关系。

对于测量噪声也同样认为符合正态分布 $P(v)\sim N(0,R)$ ， $R=E(vv^T)$ 同样为协方差矩阵，形同Q。

但建模的时候噪音是不知道的，所以我们只能测得除掉噪声其余的项，表示为 $\hat{x}_k^-$ ，这是一个估计值所以要加一个hat。此时我们没有做任何处理，只是根据上面的式子去掉噪声得来，所以在上面加一个负号，代表先验估计。

$\begin{array}{l} \hat{x}_k^-=A\hat{x}_{k-1}+Bu_{k-1}\\ z_k=Hx_k \to \hat{x}_{k_{mea}}=H^{-1}z_k \end{array}$

上式中第一行 $\hat{x}_k^-$ 为算出来的结果，第二行 $\hat{x}_{k_{mea}}$ 为测出来的结果，但他们都不具备测量噪声这一项，他们都是不太准确的。这时可以运用卡尔曼滤波器通过两个不太准确的结果得到一个准确的结果。

回忆之前数据融合的概念，对于最终的估计值， $\hat{x}_k$ （后验估计）可以表示为：

$\begin{array}{l} \hat{x}_k=\hat{x}_k^- + G(H^{-1}z_k-\hat{x}_k^-),G\in[0,1]\\ \end{array}$

当 $G=0$ ， $\hat{x}_k=\hat{x}_k^-$ ，此时更相信计算结果
当 $G=1$ ， $\hat{x}_k=H^{-1}z_k$ ，此时更相信测量结果

在许多教材中会令 $G=K_kH$ ，卡尔曼滤波器可以表示为：

$\begin{array}{l} \hat{x}_k=\hat{x}_k^- + K_k(z_k-H\hat{x}_k^-),K_k\in[0,H^{-1}]\\ \end{array}$

当 $K_k=0$ ， $\hat{x}_k=\hat{x}_k^-$ ，此时更相信计算结果
当 $K_k=H^{-1}$ ， $\hat{x}_k=H^{-1}z_k$ ，此时更相信测量结果

接下来的目标就是寻找 $K_k$ ，使得误差最小，也就是说使得估计值 $\hat{x}_k$ 趋近于实际值 $x_k$ 。很明显， $K_k$ 的取值与计算误差和测量误差息息相关，当测量误差特别大时会更相信计算出来的结果，当计算误差特别大时会更相信测量出来的结果。

令误差 $e_k=x_k-\hat{x}_k$ ，其同样符合正态分布 $P(e_k)\sim N(0,P)$

$\begin{aligned} P=E(ee^T)= \begin{bmatrix} \sigma_{e_1}^2 & \sigma_{e_1}\sigma_{e_2} \\ \sigma_{e_2}\sigma_{e_1} & \sigma_{e_2}^2 \end{bmatrix} \end{aligned}$

如果新估计出的 $x_k$ 距离实际值越小，说明误差的方差越小，说明越接近期望值0。而方差之和为P的迹 $tr(P)=\sigma_{e_1}^2+\sigma_{e_2}^2$ ，所以要想让方差最小，接下来的目标就变成了选取合适的 $K_k$ ，使得协方差矩阵P的迹最小

$\begin{aligned} P&=E\left(ee^T\right)\\ &=E\left( \left(x_k-\hat{x}_k\right)\left(x_k-\hat{x}_k\right)^T \right) \end{aligned}$

下面求 $x_k-\hat{x}_k$ ，其中的 $z_k$ 是真实测量的结果，所以 $z_k=Hx_k+v_k$ 。因为 $e_k=x_k-\hat{x}_k$ ，所以可以定义先验误差 $e_k^-=x_k-\hat{x}_k^-$

$\begin{aligned} x_k-\hat{x}_k&=x_k-(\hat{x}_k^- + K_k(z_k-H\hat{x}_k^-))\\ &=(I-K_kH)(x_k-\hat{x}_k^-)-K_kv_k \\ &=(I-K_kH)e_k^--K_kv_k \end{aligned}$

前文提到， $e_k^-$ 和 $e_k^-$ 的方差都是0，且令先验误差的协方差矩阵 $P_k^-=E(e_k^-{e_k^-}^T)$ 。此时第k步的 $P_k$ 可以整理为

$\begin{aligned} P_k&=E\left( \left(x_k-\hat{x}_k\right)\left(x_k-\hat{x}_k\right)^T \right)\\ &=E\left( \left(\left(I-K_kH\right)e_k^--K_kv_k\right)\left(\left(I-K_kH\right)e_k^--K_kv_k\right)^T \right)\\ &=P_k^--K_kHP_k^--(K_kHP_k^-)^T+K_kHP_k^-H^TK_k^T+K_kRK_k^T \end{aligned}$

此时可以计算 $P_k$ 的迹

$\begin{aligned} tr(P_k)&=tr(P_k^-)-2tr(K_kHP_k^-)+tr(K_kHP_k^-H^TK_k^T)+tr(K_kRK_k^T) \end{aligned}$

寻找k使得 $tr(P_k)$ 有最小值，对k求导并寻找极值点（求导法则略）

$\begin{aligned} \frac{dtr(P_k)}{dk}=0-2(HP_k^-)^T+2K_kHP_k^-H^T+2K_kR=0\\ \end{aligned}$ $\begin{aligned} K_k=\frac{P_k^-H^T}{HP_k^-H^T+R}\\ \end{aligned}$

至此，我们推出的 $K_k$ 就是卡尔曼增益。这也是卡尔曼滤波器中最核心的公式。

其中的R是测量噪声的协方差矩阵，R的大小代表了测量噪声方差的大小，也就是测量噪声的大小。分析 $K_k$ ：

当R很大， $K_k\to0$ ， $\hat{x}_k=\hat{x}_k^-$ ，此时更相信计算结果
当R很小， $K_k=\frac{P_k^-H^T}{HP_k^-H^T}=H^{-1},\hat{x}_k=H^{-1}z_k$ ，此时更相信测量结果

误差协方差矩阵数学推导

现在来推导卡尔曼增益 $K_k$ 中的先验误差的协方差矩阵 $P_k^-$ 。

根据前文的结论，我们可以得到真实值 $x_k$ ，先验估计 $\hat{x}_k^-$ ，后验估计 $\hat{x}_k$ ，卡尔曼增益 $K_k$

$\begin{aligned} x_k & = Ax_{k-1}+Bu_{k-1}+w_{k-1}\\ \hat{x}_k^- & = A\hat{x}_{k-1}+Bu_{k-1}\\ \hat{x}_k & = \hat{x}_k^- + K_k(z_k-H\hat{x}_k^-)\\ K_k & = \frac{P_k^-H^T}{HP_k^-H^T+R} \end{aligned}$

根据 $P_k^-$ 的定义， $P_k^-=E(e_k^-{e_k^-}^T)$ ，其中误差为真实值减估计值，

$\begin{aligned} e_k^-&=x_k-\hat{x}_k^-\\ &=Ax_{k-1}+Bu_{k-1}+w_{k-1}-A\hat{x}_{k-1}-Bu_{k-1}\\ &=A(x_{k-1}-\hat{x}_{k-1}^-)+w_{k-1}\\ &=Ae_{k-1}+w_{k-1} \end{aligned}$

则 $P_k^-$ 可以整理为：

$\begin{aligned} P_k^-&=E(e_k^-{e_k^-}^T)\\ &=E\left( (Ae_{k-1}+w_{k-1})(Ae_{k-1}+w_{k-1})^T \right)\\ &=AE(e_{k-1}^-{e_{k-1}^-}^T)A^T+E(w_{k-1}^-{w_{k-1}^-}^T)\\ &=AP_{k-1}A^T+Q \end{aligned}$

根据上式就可以利用卡尔曼滤波器估计状态变量的值了。分为以下步骤

预测
1. 先验估计
  
  $\hat{x}_k^-=A\hat{x}_{k-1}+Bu_{k-1}$
2. 先验误差协方差矩阵
  
  $P_k^-=AP_{k-1}A^T+Q$
校正
1. 卡尔曼增益
  
  $K_k=\frac{P_k^-H^T}{HP_k^-H^T+R}$
2. 后验估计
  
  $\hat{x}_k=\hat{x}_k^- + K_k(z_k-H\hat{x}_k^-)$

根据以上四步就可以得到最优估计值，也就是后验估计值 $\hat{x}_k$ 。

先验误差协方差矩阵 $P_k^-$ 中包含上一次的 $P_{k-1}^-$ 项，每次矫正厚需要更新先验误差协方差矩阵。将卡尔曼增益带入可以求得：

$\begin{aligned} P_k&=P_k^--K_kHP_k^--(K_kHP_k^-)^T+K_kHP_k^-H^TK_k^T+K_kRK_k^T\\ &=(I-K_kH)P_k^- \end{aligned}$

所以第五步为

更新先验误差协方差

$P_k=(I-K_kH)P_k^-$

以上就是完整的卡尔曼滤波器的五个公式。

可以看到，每次预测都会用到上一次的结果，所以在最开始要赋予初值 $\hat{x}_0$ 和 $P_0$ ，初值的选取会在下文提及。

扩展卡尔曼滤波

前文讲到，卡尔曼滤波器在线性系统里可以得到最优估计值。对于非线性系统，可以将其线性化再进行处理，这种滤波器叫做扩展卡尔曼滤波器（Extend Kalman Filter），简称EKF。

线性系统可以表示为：

$\begin{array}{l} x_k=Ax_{k-1}+Bu_{k-1}+w_{k-1}\\ z_k=Hx_k+v_k \end{array}$

而非线性系统，无法用线性的状态空间方程表达，而是可以表示为：

$\begin{array}{l} x_k=f(x_{k-1},u_{k-1},w_{k-1})\\ z_k=h(x_k,v_k) \end{array}$

其中f为过程方程，h为测量方程，这是两个非线性的表达形式。注意无论是线性还是非线性，误差v和w都是符合正态分布的。但正态分布的随机变量通过非线性系统以后就不再是正态分布的了。所以如果还想对非线性系统进行卡尔曼滤波，需要对其线性化（Linearization），用泰勒级数展开，不赘述过程只给出结论：

$\begin{aligned} f(x)=f(x_0)+\frac{\partial f}{\partial x}(x-x_0) \end{aligned}$

如果需要线性化一个系统，需要找到一个点（Operating Point），在这个点附近进行线性化。对于非线性系统来说最好的线性化的点就是它的真实点，但由于系统有误差，无法知道真实值，所以无法在真实点进行线性化，所以过程方程 $f(x_k)$ 只能在 $\hat{x}_{k-1}$ 附近，也就是k-1时刻（上一次）的后验估计附近进行线性化。

由于不知道误差 $w_{k-1}$ 是多少，所以将其假设为0，定义 $f(\hat{x}_{k-1},u_{k-1},0)=\tilde x_k$ ，可以得到

$\begin{aligned} x_k & = f(\hat{x}_{k-1},u_{k-1},0)+A_k(x_{k-1}-\hat{x}_{k-1})+W_kw_{k-1}\\ A_k &= \frac{\partial f}{\partial x}|_{\hat{x}_{k-1},u_{k-1}}\qquad W_k = \frac{\partial f}{\partial w}|_{\hat{x}_{k-1},u_{k-1}} \end{aligned}$

例：

$\begin{aligned} x_1&=x_1+sinx_2=f_1\\ x_2&=x_1^2=f_2\\ A_k&=\frac{\partial f}{\partial x}|_{\hat{x_1}_{k-1},\hat{x_2}_{k-1}}\\&= \begin{bmatrix} \frac{\partial f_1}{\partial x_1} & \frac{\partial f_1}{\partial x_2} \\ \frac{\partial f_2}{\partial x_1} & \frac{\partial f_2}{\partial x_2} \end{bmatrix}|_{\hat{x_1}_{k-1},\hat{x_2}_{k-1}}\\&= \begin{bmatrix} 1 & cosx_2 \\ 2x_1 & 0 \end{bmatrix}|_{\hat{x_1}_{k-1},\hat{x_2}_{k-1}}\\&= \begin{bmatrix} 1 & cos\hat{x_2}_{k-1} \\ 2\hat{x_1}_{k-1} & 0 \end{bmatrix} \end{aligned}$

可以看出，A矩阵随着K的变化而变化，所以每次要重新计算A矩阵。

同理对于测量方程， $z_k$ 在 $\tilde x_k$ 附近进行线性化。由于不知道误差 $v_k$ ，所以将其假设为0，定义 $h(\hat{x}_k,0)=\tilde z_k$

$\begin{aligned} z_k&=h(\tilde x,0)+H_k(x_k-\tilde{x}_k)+V_kv_k\\ H_k&=\frac{\partial h}{\partial x}|_{\hat{x}_k}\qquad V_k=\frac{\partial h}{\partial v}|_{\hat{x}_k}\\ \end{aligned}$

这样就把非线性系统线性化了：

$\begin{aligned} x_k&=\tilde x_k+A_k(x_{k-1}-\hat{x}_{k-1})+W_kw_{k-1}\\ z_k&=\tilde z_k+H(x_k-\tilde{x}_k)+Vv_k \end{aligned}$

其中的 $W_kw_{k-1}$ 和 $Vv_k$ 也都是正态分布（ $WQW^T$ 相当于矩阵中W的平方）：

$\begin{aligned} P(w) &\sim N(0,R)\\ P(Ww_{k-1}) &\sim N(0,WQW^T)\\ P(Vv_k) &\sim N(0,VRV^T) \end{aligned}$

将卡尔曼滤波器的线性化部分替换成对应非线性的部分，就可以得到扩展卡尔曼滤波器的五个公式：

预测
1. 先验估计
  
  $\hat{x}_k^-=f(\hat{x}_{k-1},u_{k-1},0)$
2. 先验误差协方差矩阵
  
  $P_k^-=AP_{k-1}A^T+WQW^T$
校正
1. 卡尔曼增益
  
  $K_k=\frac{P_k^-H^T}{HP_k^-H^T+VRV^T}$
2. 后验估计
  
  $\hat{x}_k=\hat{x}_k^- + K_k(z_k-h(\hat{x}_k,0))$

更新先验误差协方差

$P_k=(I-K_kH)P_k^-$