FOC控制原理——Clark变换和Park变换

Clark变换

原理

Clark变换就是把三向坐标系变成直角坐标系

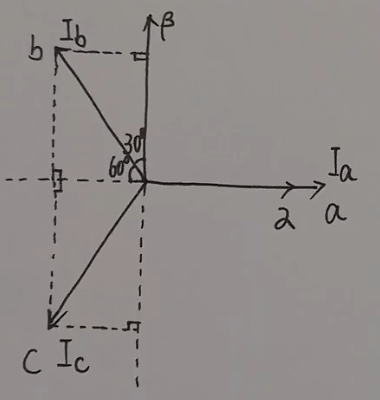
已知三向坐标系 $(I_a,I_b,I_c)$ ，这三个基向量不是正交的，所以可以将其正交化为一个直角坐标系，命名为 $\alpha-\beta$ 坐标系，变换公式为：

$\left\{\begin{array}{l} \begin{aligned} I_\alpha&=I_a-I_b\text{cos}60-I_c\text{cos}60 \\ &=I_a-\frac{1}{2}I_b-\frac{1}{2}I_c \end{aligned} \\ \begin{aligned} I_\beta&=I_b\text{cos}30-I_c\text{cos}30 \\ &=\frac{\sqrt3}{2}I_b-\frac{\sqrt3}{2}I_c \end{aligned} \end{array}\right.$

可以将其整理成矩阵形式：

$\left[\begin{array}{c} I_{\alpha} \\ I_{\beta} \end{array}\right]= \left[\begin{array}{ccc} 1 & -\frac{1}{2} & -\frac{1}{2} \\ 0 & \frac{\sqrt{3}}{2} & -\frac{\sqrt{3}}{2} \end{array}\right] \left[\begin{array}{c} I_{a} \\ I_{b} \\ I_{c} \end{array}\right]$

由基尔霍夫电流定律， $I_a+I_b+I_c=0$ ，故也可整理为：

$\left\{\begin{array}{l} I_\alpha=\frac{3}{2}I_a \\ I_\beta=\frac{\sqrt3}{2}I_a+\sqrt3I_b \end{array}\right.$

反Clark变换则将三向信号转换为两向信号，根据上式可以解得

$\left[\begin{array}{c} I_{a} \\ I_{b} \\ I_{c} \end{array}\right]= \left[\begin{array}{ccc} \frac{2}{3} & 0 \\ -\frac{1}{3} & \frac{1}{\sqrt{3}} \\ -\frac{1}{3} & -\frac{1}{\sqrt{3}} \end{array}\right] \left[\begin{array}{c} I_{\alpha} \\ I_{\beta} \end{array}\right]$

也可通过计算Clark变换常数矩阵的伪逆来确定反Clark变换的常数矩阵（使用MATLAB中的 pinv()函数）

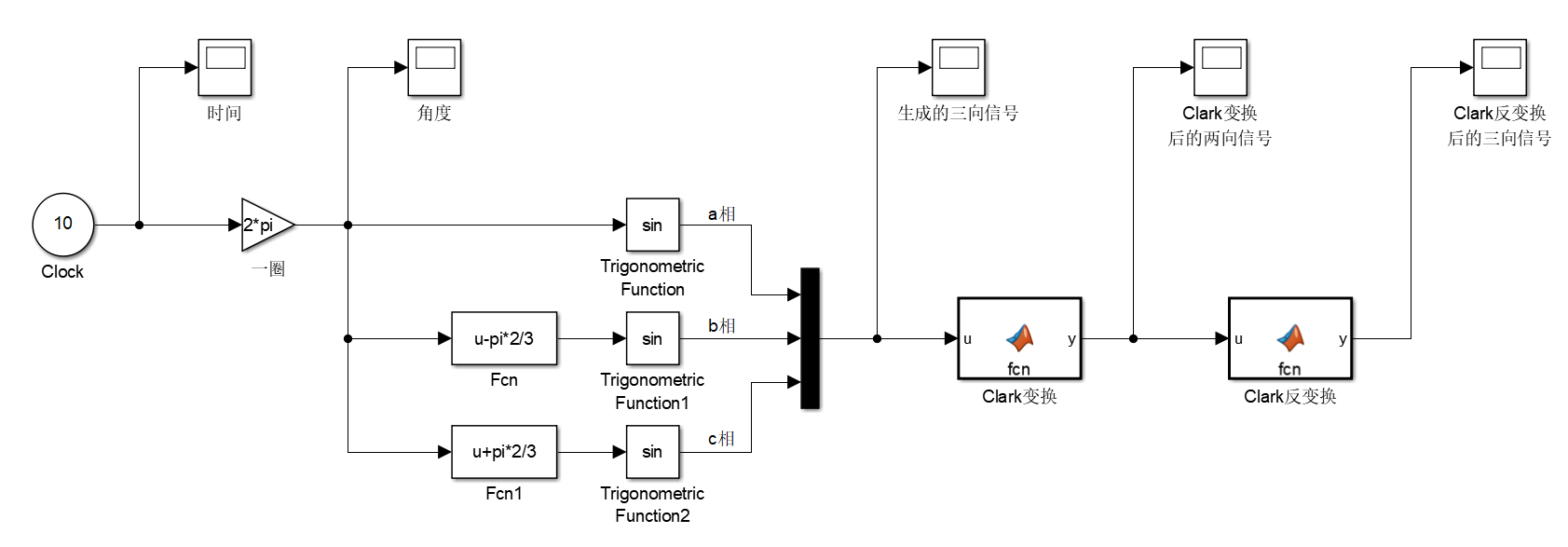
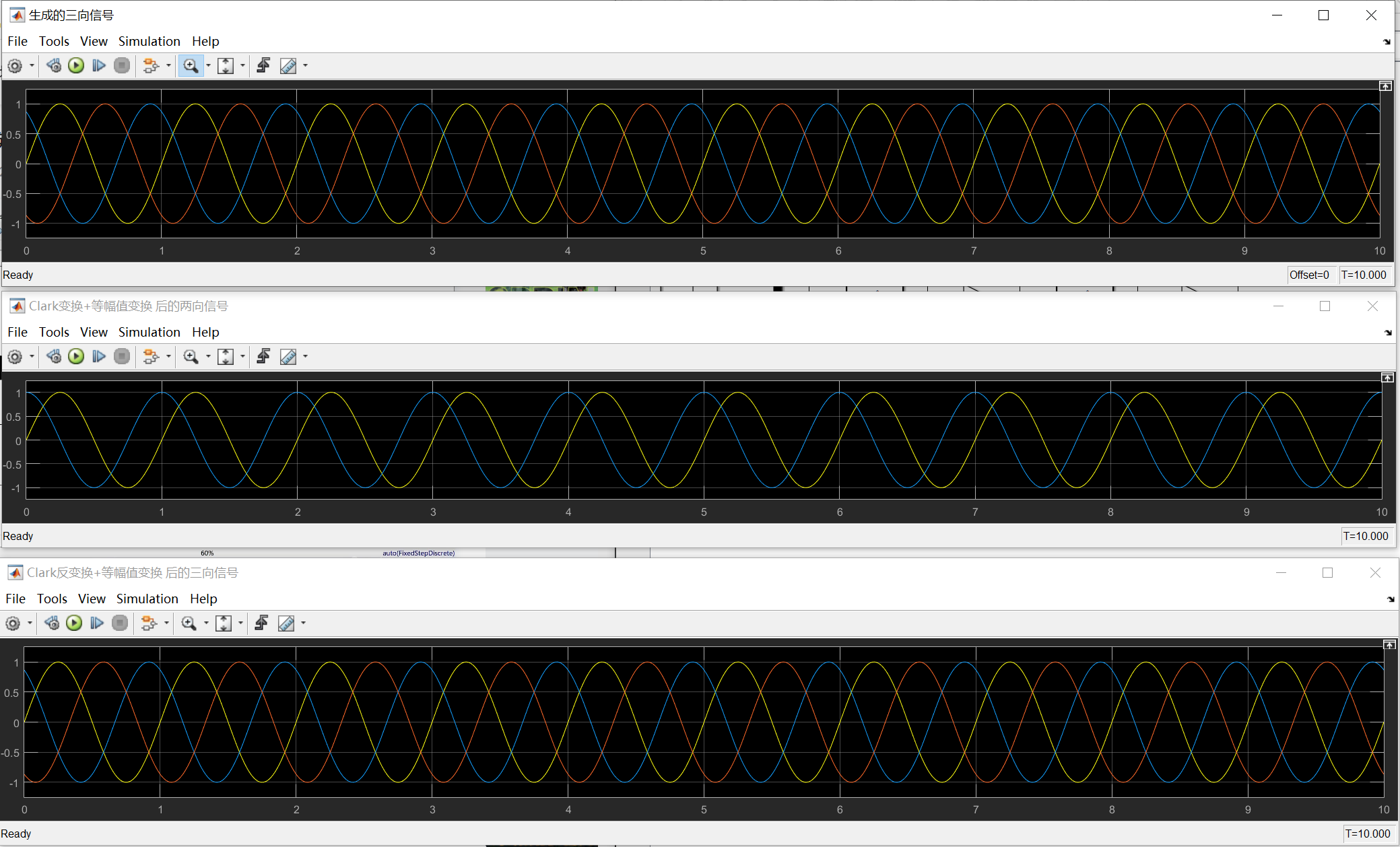
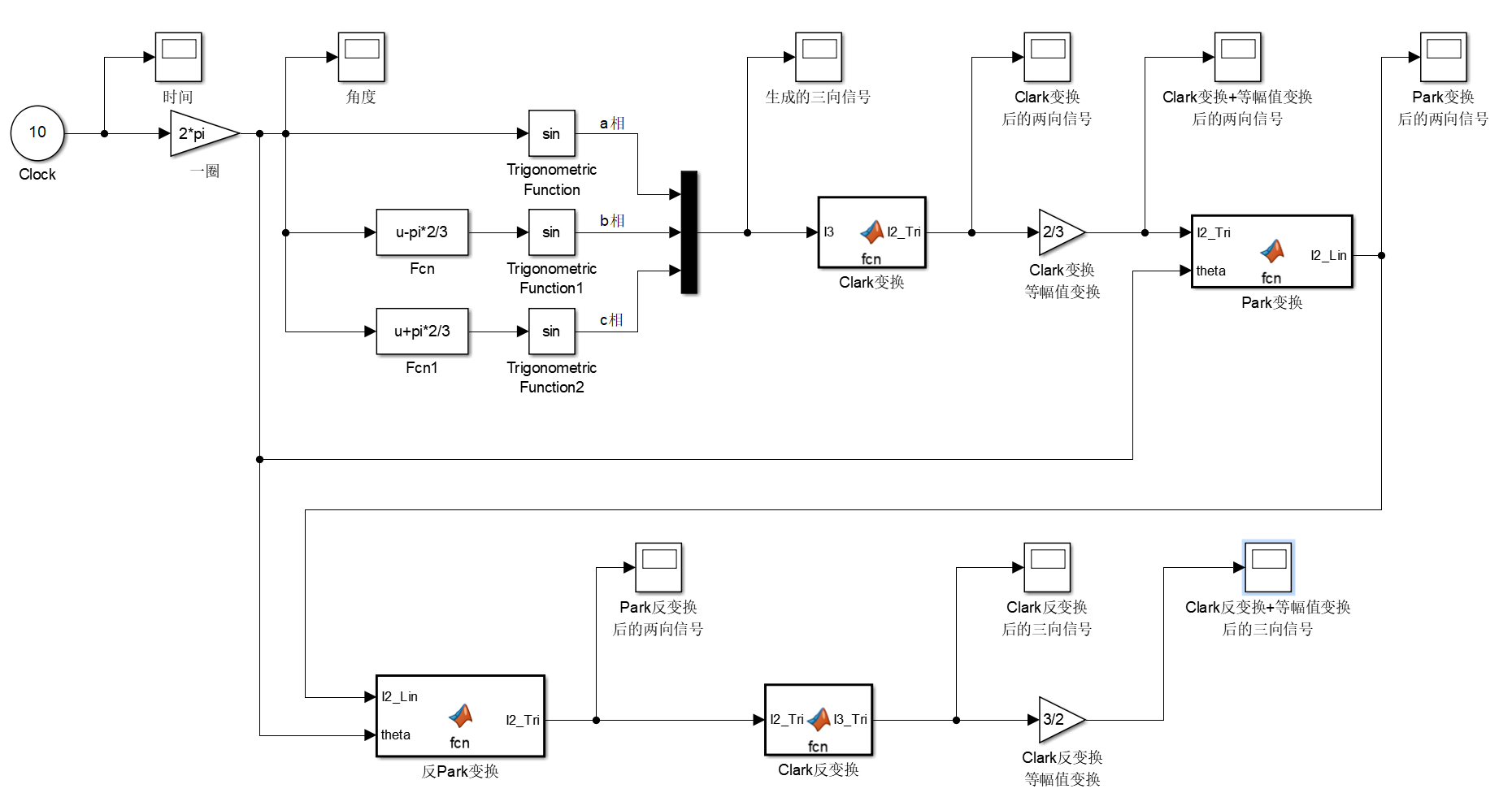
Simulink仿真

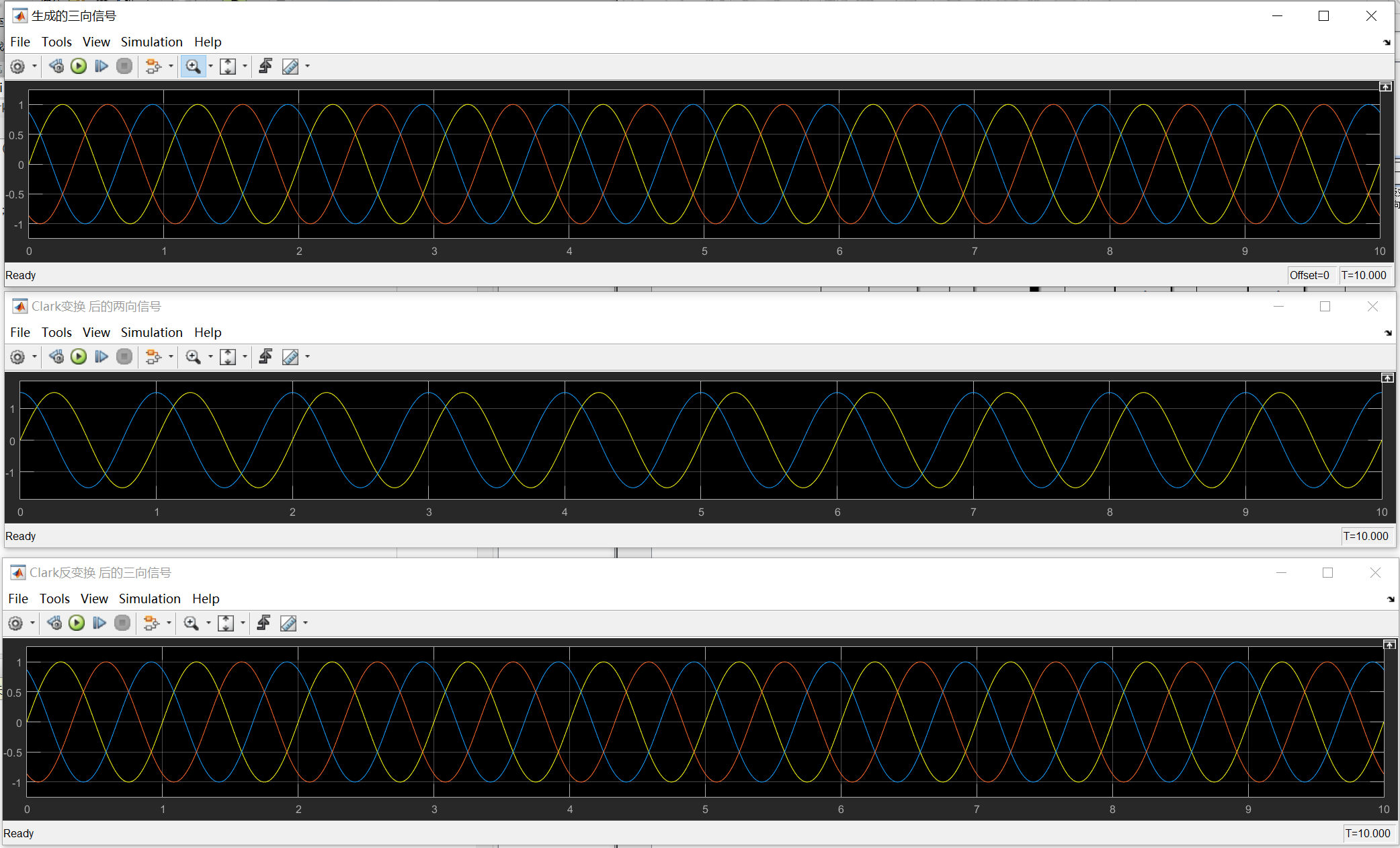
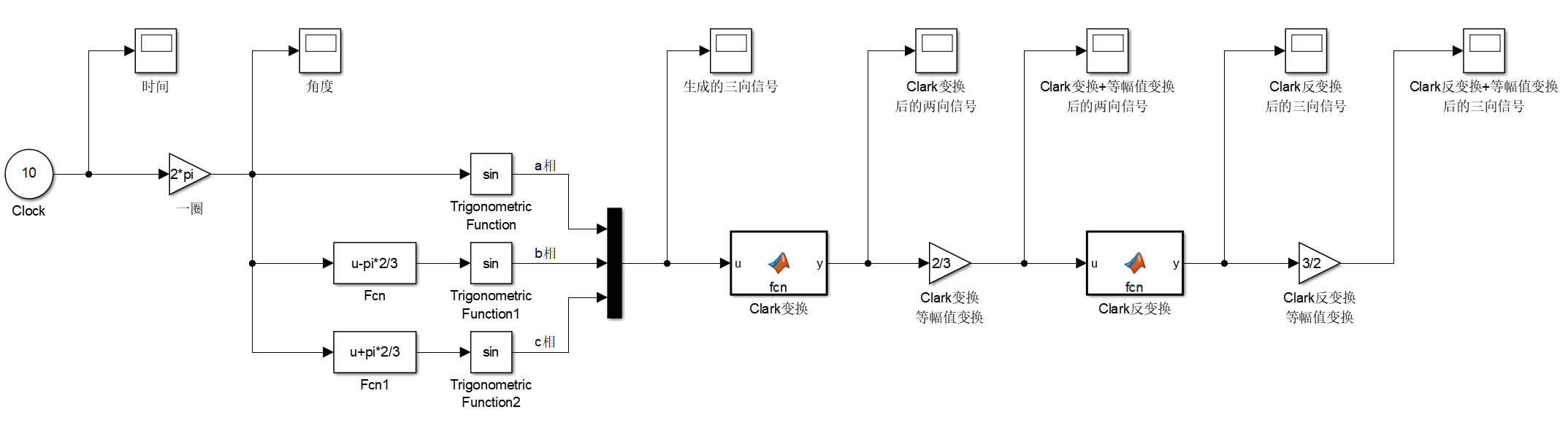
通过图像可以看到，输入信号的幅值为1，经过Clark变换后的图像幅值变为1.5，即变为 $\frac{3}{2}$ 倍；进行反Clark变换后幅值又变为1.5，即变为 $\frac{2}{3}$ 倍。所以要进行等幅值变换。修改仿真：

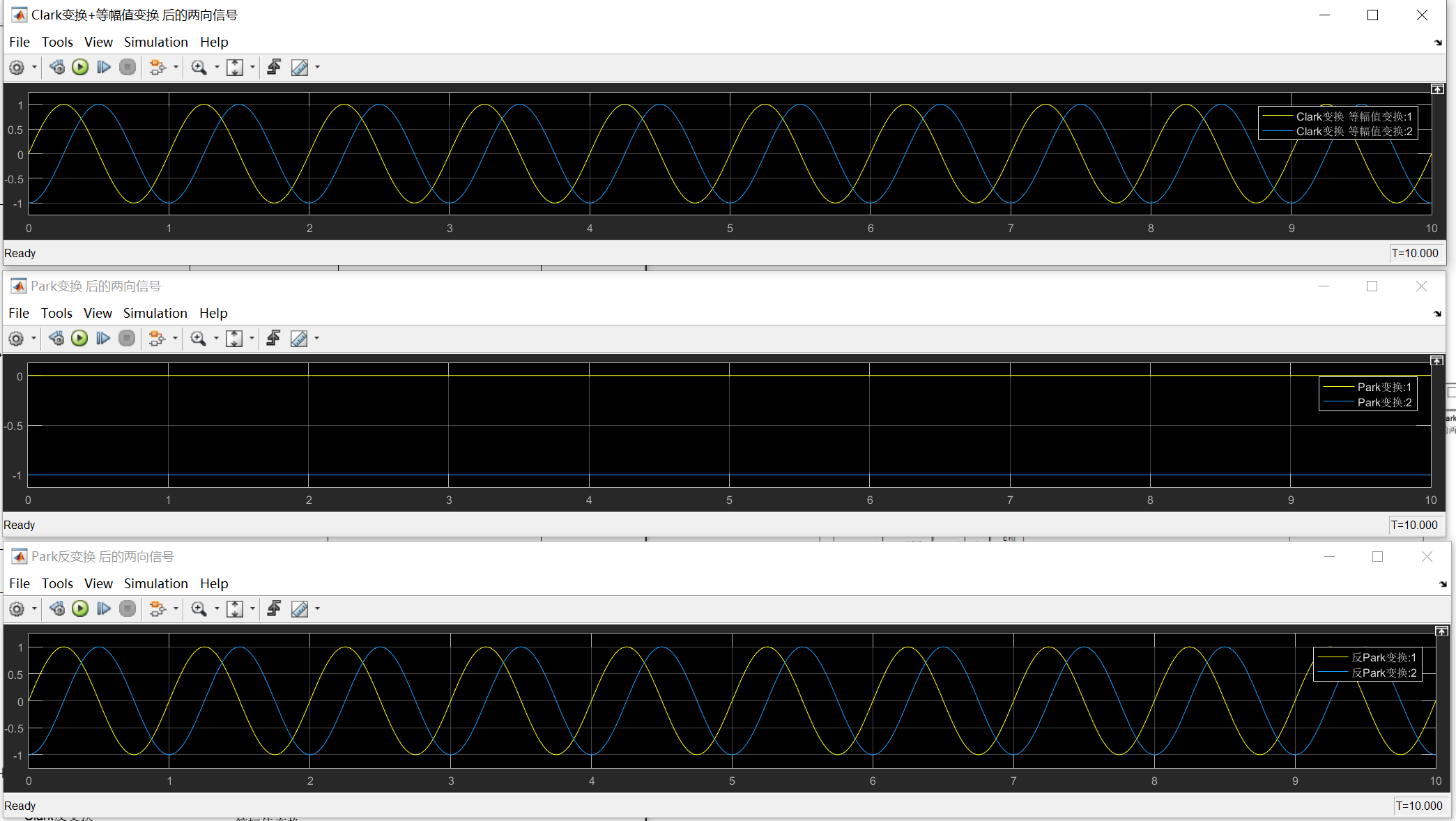
可以看到，经过等幅值变换后，幅值统一为1。

Park变换

原理

Park变换可以将正弦变量线性化

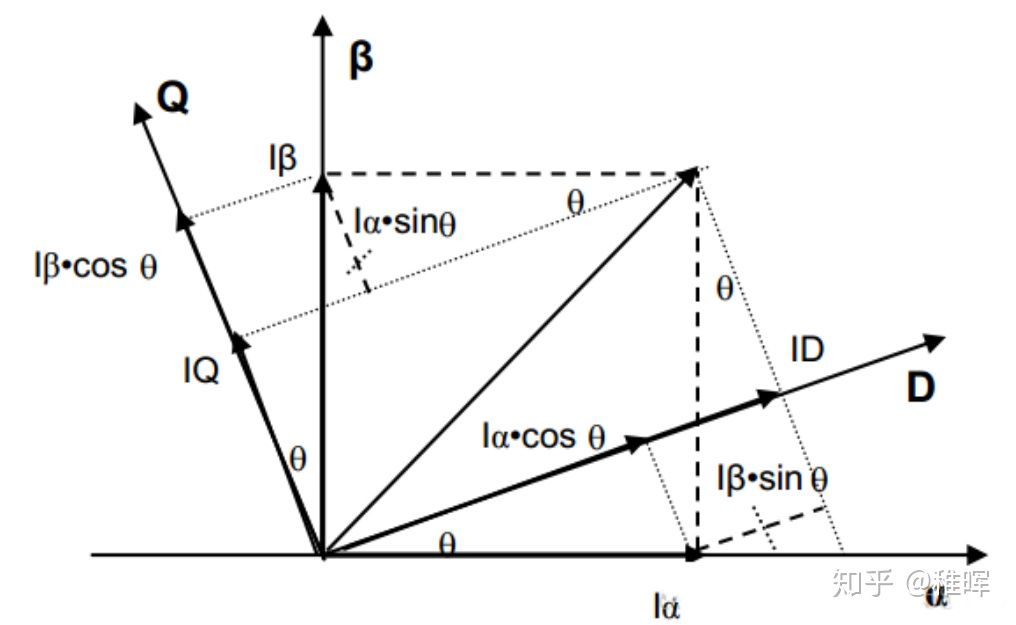
将 $\alpha-\beta$ 坐标系旋转 $\theta$ 度变为 $d-q$ 坐标系， $d$ 指向转子中心， $q$ 指向切线方向，其中 $\theta$ 是转子当前的角度。如下图

也就是说 $d-q$ 坐标系始终跟着转子旋转。

则可以写出

$\left\{\begin{array}{l} I_{d}=I_{\alpha} \cos (\theta)+I_{\beta} \sin (\theta) \\ I_{q}=-I_{\alpha} \sin (\theta)+I_{\beta} \cos (\theta) \end{array}\right.$

整理成矩阵形式

$\left[\begin{array}{l} I_{d} \\ I_{q} \end{array}\right]= \left[\begin{array}{cc} \cos \theta & \sin \theta \\ -\sin \theta & \cos \theta \end{array}\right] \left[\begin{array}{l} I_{\alpha} \\ I_{\beta} \end{array}\right]$

所以如果 $d$ 轴为0，则功率全部输出在 $q$ 轴上。

同理，可以求得反Park变换

$\left[\begin{array}{l} I_{\alpha} \\ I_{\beta} \end{array}\right]= \left[\begin{array}{cc} \cos \theta & -\sin \theta \\ \sin \theta & \cos \theta \end{array}\right] \left[\begin{array}{l} I_{d} \\ I_{q} \end{array}\right]$