OpenCV直方图均衡化

直方图均衡化，是对图像进行非线性拉伸，使得一定范围内像素值的数量的大致相同。这样原来直方图中的封顶部分对比度得到了增强，而两侧波谷的对比度降低，输出的直方图是一个较为平坦的分段直方图。直方图均衡化适用于增强直方图呈尖峰分布的图像。

几种图片的的直方图均衡化处理效果

欠曝

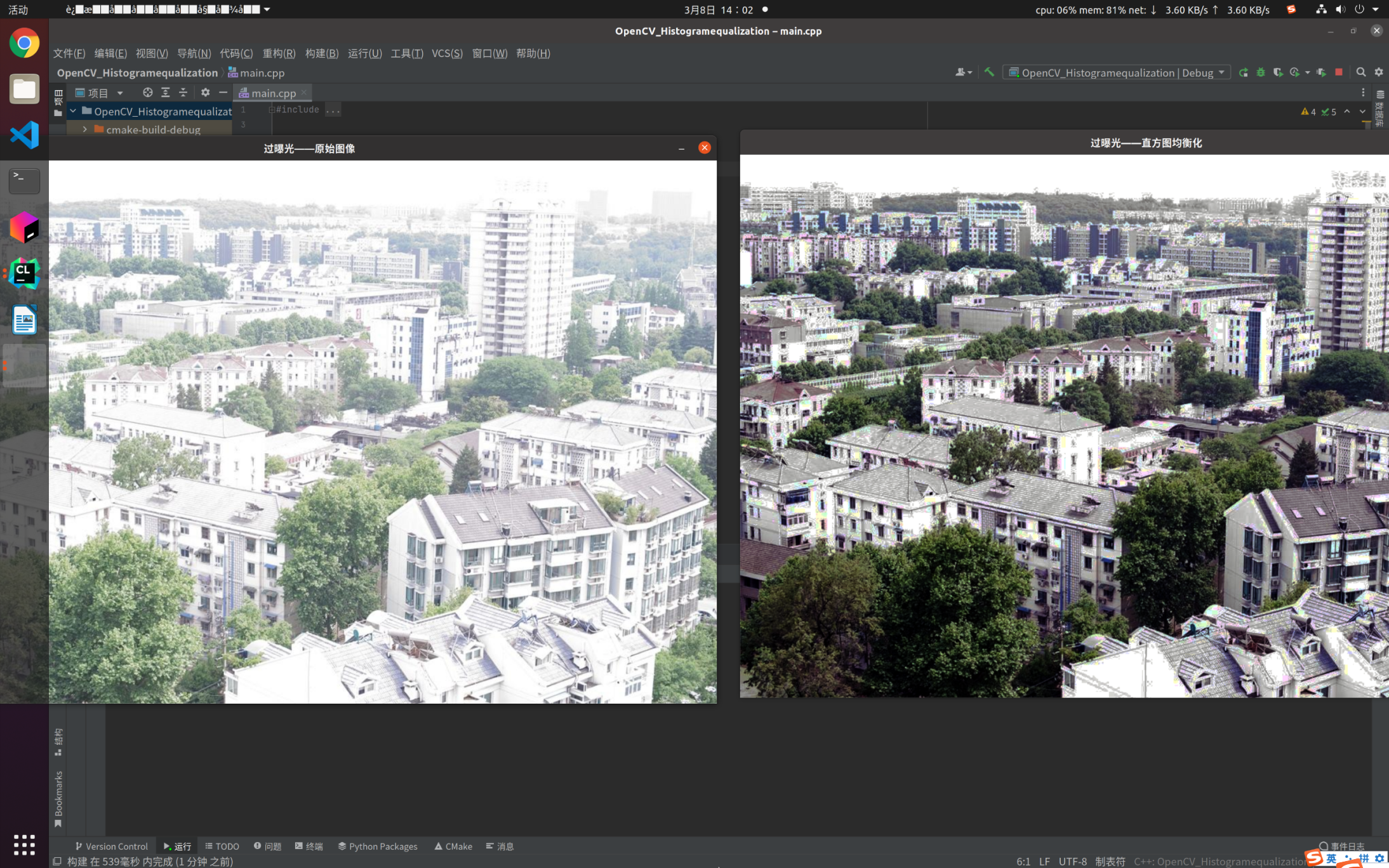
过曝

从上面两个图片可以看到，直方图均衡化对于背景和前景都太亮或者太暗的图像效果较好，而且这是一个可逆操作，如果已知均衡化函数，那么就可以恢复原始的直方图。但缺点是直方图均衡化对处理的数据不加选择，它可能会增加背景噪声的对比度并且降低有用信号的对比度；变换后图像的灰度级减少，某些细节消失；某些图像，如直方图有高峰，经处理后对比度不自然的过分增强。

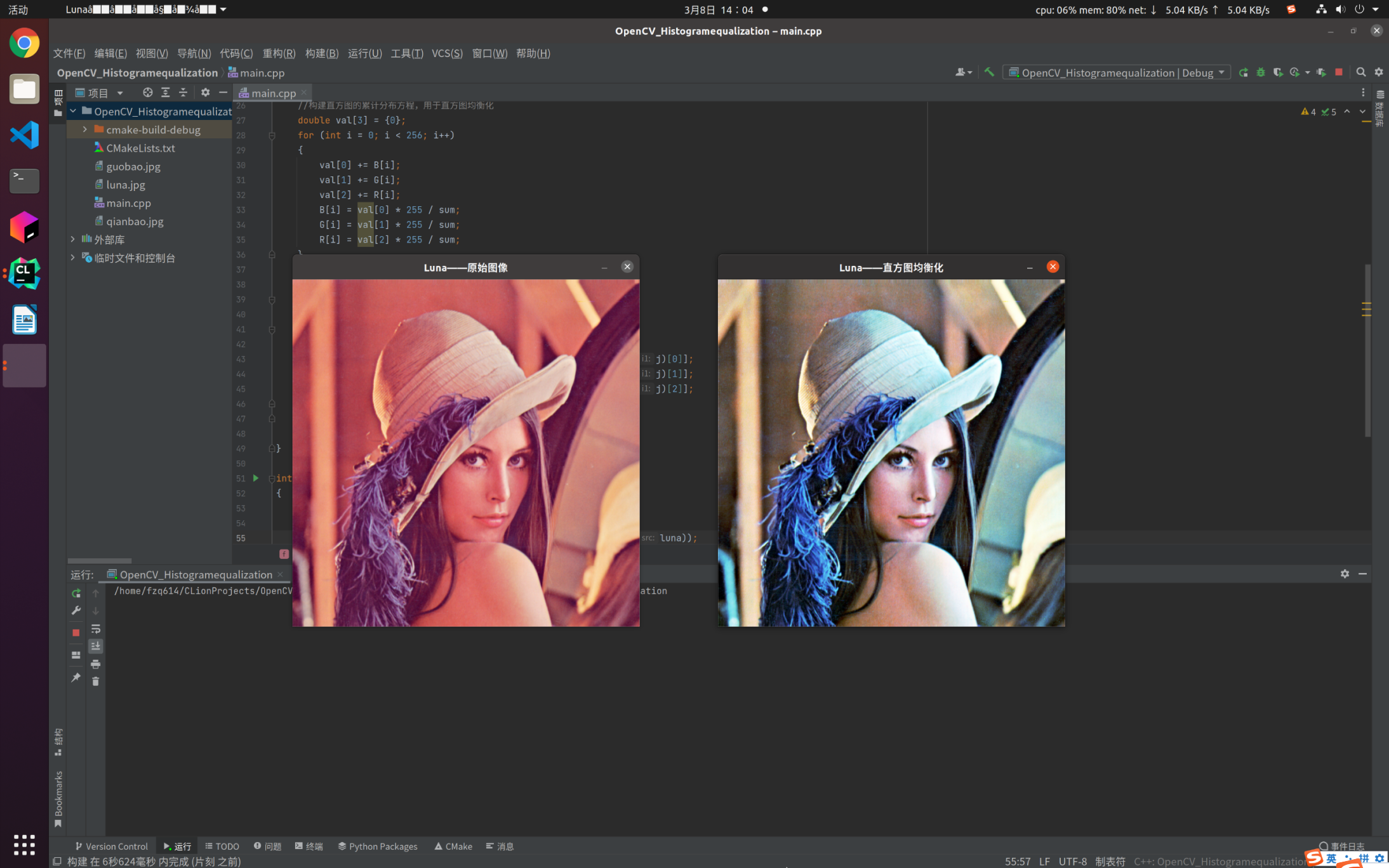
下面再贴一张Luna的处理图：

代码

#include <iostream>
#include<opencv2/opencv.hpp>

using namespace cv;
using namespace std;

//直方图均衡化
Mat Histogramequalization(Mat src)
{
	int R[256] = {0};
	int G[256] = {0};
	int B[256] = {0};
	int rows = src.rows;
	int cols = src.cols;
	int sum = rows * cols;
	//统计直方图的RGB分布
	for (int i = 0; i < rows; i++)
	{
		for (int j = 0; j < cols; j++)
		{
			B[src.at<Vec3b>(i, j)[0]]++;
			G[src.at<Vec3b>(i, j)[1]]++;
			R[src.at<Vec3b>(i, j)[2]]++;
		}
	}
	//构建直方图的累计分布方程，用于直方图均衡化
	double val[3] = {0};
	for (int i = 0; i < 256; i++)
	{
		val[0] += B[i];
		val[1] += G[i];
		val[2] += R[i];
		B[i] = val[0] * 255 / sum;
		G[i] = val[1] * 255 / sum;
		R[i] = val[2] * 255 / sum;
	}
	//归一化直方图
	Mat dst(rows, cols, CV_8UC3);
	for(int i = 0; i < rows; i++)
	{
		for(int j = 0; j < cols; j++)
		{
			dst.at<Vec3b>(i, j)[0] = B[src.at<Vec3b>(i, j)[0]];
			dst.at<Vec3b>(i, j)[1] = G[src.at<Vec3b>(i, j)[1]];
			dst.at<Vec3b>(i, j)[2] = R[src.at<Vec3b>(i, j)[2]];
		}
	}
	return dst;
}

int main()
{
	Mat luna = imread("./luna.jpg");
	imshow("Luna——原始图像", luna);
	imshow("Luna——直方图均衡化", Histogramequalization(luna));

	Mat guobao = imread("./guobao.jpg");
	imshow("过曝光——原始图像", guobao);
	imshow("过曝光——直方图均衡化", Histogramequalization(guobao));

	Mat qianbao = imread("./qianbao.jpg");
	imshow("欠曝光——原始图像", qianbao);
	imshow("欠曝光——直方图均衡化", Histogramequalization(qianbao));

	waitKey();
	return 0;
}