四足机器人传统控制方法学习笔记

运动学与动力学

单腿运动学

正运动学

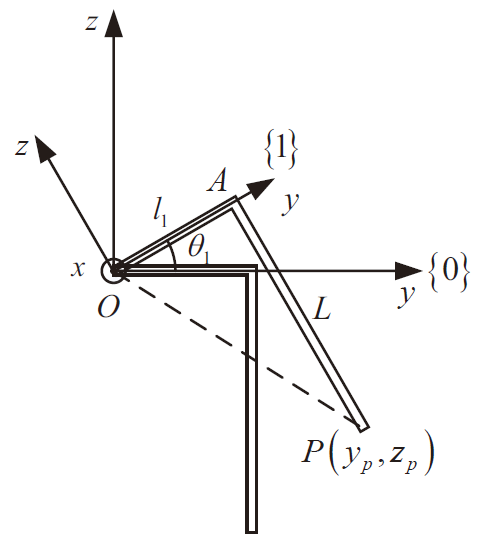
目标：已知三个关节的角度 $(\theta_1,\theta_2,\theta_3)$ ，需要求出足端位置 $(x,y,z)$

$\begin{aligned} \boldsymbol{T}_{01}&= \begin{bmatrix} \mathrm{rot}_x(\theta_1) & \boldsymbol{0}_{3\times1} \\ \boldsymbol{0}_{3\times3} & 1 \end{bmatrix}= \begin{bmatrix} 1 & 0 & 0 & 0 \\ 0 & \cos(\theta_1) & -\sin(\theta_1) & 0 \\ 0 & \sin(\theta_1) & \cos(\theta_1) & 0 \\ 0 & 0 & 0 & 1 \end{bmatrix}\\ \boldsymbol{T}_{12}&= \begin{bmatrix} \mathrm{rot}_y(\theta_2) & \boldsymbol{0}_{3\times1} \\ \boldsymbol{0}_{3\times3} & 1 \end{bmatrix}= \begin{bmatrix} \cos(\theta_2) & 0 & \sin(\theta_2) & 0 \\ 0 & 1 & 0 & 0 \\ -\sin(\theta_2) & 0 & \cos(\theta_2) & 0 \\ 0 & 0 & 0 & 1 \end{bmatrix}\\ \boldsymbol{T}_{23}&= \begin{bmatrix} \mathrm{rot}_y(\theta_3) & \left[\begin{matrix}0\\l_1\\l_2\end{matrix}\right] \\ \boldsymbol{0}_{3\times3} & 1 \end{bmatrix}= \begin{bmatrix} \cos(\theta_3) & 0 & \sin(\theta_3) & 0 \\ 0 & 1 & 0 & l_1 \\ -\sin(\theta_3) & 0 & \cos(\theta_3) & l_2 \\ 0 & 0 & 0 & 1 \end{bmatrix} \quad \begin{aligned} l_1 &= \left\{ \begin{aligned}-l_{abad}&,\text{right}\\l_{abad}&,\text{left}\end{aligned}\right. \\ l_2 &= -l_{hip}\end{aligned}\\ \boldsymbol{p}_3 &= \begin{bmatrix}0\\0\\l_3\\1\end{bmatrix} \quad \begin{aligned}l_3=-l_{knee}\end{aligned} \end{aligned}$

根据以上变换即可求出足端位置：

$\begin{bmatrix} x_p\\y_p\\z_p\\1 \end{bmatrix}= \begin{bmatrix} l_3\sin(\theta_1+\theta_2)+l_2\sin(\theta_2)\\ -l_3\sin(\theta_1)\cos(\theta_2+\theta_3)+l_1\cos(\theta_1)-l_2\cos(\theta_2)\sin(\theta_1)\\ l_3\cos(\theta_1)\cos(\theta_2+\theta_3)+l_1\sin(\theta_1)+l_2\cos(\theta_1)\cos(\theta_2)\\ 1 \end{bmatrix} \tag{1}$

逆运动学

目标：已知足端位置 $(x,y,z)$ ，需要求出三个关节的角度 $(\theta_1,\theta_2,\theta_3)$

求 $\theta_1$

$\begin{aligned} \boldsymbol{P}_0 &= \boldsymbol{R}_{01} \boldsymbol{P}_1\\ \begin{bmatrix} y_p\\z_p \end{bmatrix}&= \begin{bmatrix} \cos(\theta_1)&-\sin(\theta_1)\\ \sin(\theta_1)&\cos(\theta_1) \end{bmatrix} \begin{bmatrix} L\\-L \end{bmatrix} \end{aligned}$
整理得
$\left\{ \begin{aligned} y_p&=l_1\cos(\theta_1)+L\sin(\theta_1)\\ z_p&=l_1\sin(\theta_1)-L\cos(\theta_1) \end{aligned} \right.\Rightarrow \left\{ \begin{aligned} \frac{y_p}{\cos(\theta_1)}=l_1+L\tan(\theta_1)\\ \frac{z_p}{\cos(\theta_1)}=l_1\tan(\theta_1)-L \end{aligned} \right.$
由于 $z_p \ne 0$ ，可以推出 $\frac{y_p}{z_p}=\frac{l_1+L\tan(\theta_1)}{l_1\tan(\theta_1)-L}$ ，从而可以解出 $\tan(\theta_1)=\frac{z_pl_1+y_pL}{y_pl_1-z_pL}$ ，即 $\theta_1=\arctan\left(\frac{z_pl_1+y_pL}{y_pl_1-z_pL}\right)$
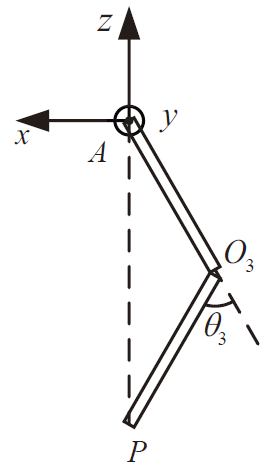
求 $\theta_3$ （余弦定理）

从图中可以得
$\begin{aligned} \angle{AO_3P}&=\arccos\left(\frac{\left|\overrightarrow{O_3A}\right|^2+\left|\overrightarrow{O_3P}\right|^2-\left|\overrightarrow{AP}\right|^2}{2\left|\overrightarrow{O_3A}\right|\left|\overrightarrow{O_3P}\right|}\right) \quad \text{其中}\left\{\begin{aligned} \left|\overrightarrow{AP}\right|&=\sqrt{x_p^2+y_p^2+z_p^2-l_1^2}\\ \left|\overrightarrow{O_3A}\right|&=\sqrt{l_2}\\ \left|\overrightarrow{O_3P}\right|&=\sqrt{l_3} \end{aligned}\right.\\ &=\arccos\left( \frac{(l_1+l_2+l_3)-(x_p^2+y_p^2+z_p^2)}{2\sqrt{l_2l_3}} \right) \end{aligned}$
则可求出 $\left|\theta_3\right|=\pi-\angle{AO_3P}$ ，选定逆时针为正，则 $\theta_3=\left|\theta_3\right|$
求 $\theta_2$

由前文的正运动学公式 $(1)$ 可得：
$\left\{\begin{aligned} x_{p} &= \left(l_{3} \cos \theta_{3}+l_{2}\right) \sin \theta_{2}+l_{3} \sin \theta_{3} \cos \theta_{2}\\ y_{p} &= -l_{3} \sin \theta_{1} \cos \left(\theta_{2}+\theta_{3}\right)+l_{1} \cos \theta_{1}-l_{2} \cos \theta_{2} \sin \theta_{1}\\ z_{p} &= l_{3} \cos \theta_{1} \cos \left(\theta_{2}+\theta_{3}\right)+l_{1} \sin \theta_{1}+l_{2} \cos \theta_{1} \cos \theta_{2} \end{aligned}\right.$
可以求出
$\begin{align} y_{p} \sin \theta_{1}-z_{p} \cos \theta_{1} & = -l_{3} \cos \left(\theta_{2}+\theta_{3}\right)\left(\sin ^{2} \theta_{1}+\cos ^{2} \theta_{1}\right)-l_{2} \cos \theta_{2}\left(\sin ^{2} \theta_{1}+\cos ^{2} \theta_{1}\right) \\ & = l_{3} \sin \theta_{3} \sin \theta_{2}-\left(l_{3} \cos \theta_{3}+l_{2}\right) \cos \theta_{2} \end{align}$
同除 $x_p$
$\begin{aligned} \frac{y_{p} \sin \theta_{1}-z_{p} \cos \theta_{1}}{x_{p}} & = \frac{l_{3} \sin \theta_{3} \sin \theta_{2}-\left(l_{3} \cos \theta_{3}+l_{2}\right) \cos \theta_{2}}{\left(l_{3} \cos \theta_{3}+l_{2}\right) \sin \theta_{2}+l_{3} \sin \theta_{3} \cos \theta_{2}} \end{aligned}$
令 $\left\{\begin{aligned}
a_1&=y_p \sin \theta_1-z_p \cos \theta_1 \\
a_2&=x_p \\
m_1&=l_3 \sin \theta_3 \\
m_2&=l_3 \cos \theta_3+l_2
\end{aligned}
\right.$ ，上式可以表示为：
$\begin{aligned} \frac{a_1}{a_2}&=\frac{m_1 \sin \theta_2-m_2 \cos \theta_2}{m_1 \cos \theta_2+m_2 \sin \theta_2} \\&=\frac{m_1 \tan \theta_2-m_2}{m_1+m_2 \tan \theta_2}\quad \end{aligned}$
同除 $\cos(\theta_2)$ 可以解得：
$\begin{aligned} \tan(\theta_2)=\frac{a_1 m_1+a_2 m_2}{a_2 m_1-a_1 m_2} \end{aligned}$
即可求出 $\theta_2$ ：
$\begin{aligned} \theta_2=\arctan \left(\frac{a_1 m_1+a_2 m_2}{a_2 m_1-a_1 m_2}\right) \end{aligned}$

至此完成逆运动学求解。

雅可比矩阵

对前文的正运动学公式 $(1)$ 求导：

$\left\{\begin{aligned} \dot{x}_p= & 0 \cdot \dot{\theta}_1+\left(l_3 \cos \left(\theta_2+\theta_3\right)+l_2 \cos \theta_2\right) \cdot \dot{\theta}_2+l_3 \cos \left(\theta_2+\theta_3\right) \cdot \dot{\theta}_3 \\ \dot{y}_p= & \left(-l_1 \sin \theta_1-l_2 \cos \theta_1 \cos \theta_2-l_3 \cos \theta_1 \cos \left(\theta_2+\theta_3\right)\right) \cdot \dot{\theta}_1+ \\ & \left(l_2 \sin \theta_1 \sin \theta_2+l_3 \sin \theta_1 \sin \left(\theta_2+\theta_3\right)\right) \cdot \dot{\theta}_2 + l_3 \sin \theta_1 \sin \left(\theta_2+\theta_3\right) \cdot \dot{\theta}_3 \\ \dot{z}_p= & \left(l_1 \cos \theta_1-l_2 \sin \theta_1 \cos \theta_2-l_3 \sin \theta_1 \cos \left(\theta_2+\theta_3\right)\right) \cdot \dot{\theta}_1+ \\ & \left(-l_2 \cos \theta_1 \sin \theta_2-l_3 \cos \theta_1 \sin \left(\theta_2+\theta_3\right)\right) \cdot \dot{\theta}_2+\left(-l_3 \cos \theta_1 \sin \left(\theta_2+\theta_3\right)\right) \cdot \dot{\theta}_3 \end{aligned} \right.$

整理成矩阵形式：

$\begin{bmatrix}\dot{x}_{p}\\ \dot{y}_{p}\\ \dot{z}_{p}\end{bmatrix}=\begin{bmatrix}J_{11} & J_{12} & J_{13}\\ J_{21} & J_{22} & J_{23}\\ J_{31} & J_{32} & J_{33}\end{bmatrix}\cdot\begin{bmatrix}\dot{\theta}_1\\ \dot{\theta}_2\\ \dot{\theta}_3\end{bmatrix}=\boldsymbol{J}\cdot\begin{bmatrix}\ddot{\theta}_1\\ \dot{\theta}_2\\ \dot{\theta}_3\end{bmatrix} \tag{2}$

对其求逆即可得到逆雅可比

$\begin{bmatrix}\dot{\theta_1}\\\dot{\theta_2}\\\dot{\theta_3}\end{bmatrix}=\boldsymbol{J}^{-1}\begin{bmatrix}\dot{x}_p\\\dot{y}_p\\\dot{z}_p\end{bmatrix} \tag{3}$

单腿静力学

当机器人腿部静止于地面，其关节力矩 $\boldsymbol{\tau}=\begin{bmatrix}\tau_1\\\tau_2\\\tau_3\end{bmatrix}$ ，足端对地面的作用力 $\boldsymbol{F}=\begin{bmatrix}F_x\\F_y\\F_z\end{bmatrix}$

可以得到其关系

$\tau_1\dot{\theta_1}+\tau_2\dot{\theta_2}+\tau_3\dot{\theta_3}=F_x\dot{x_p}+F_y\dot{y_p}+F_z\dot{z_p}$

整理成矩阵形式

$\begin{aligned}\begin{bmatrix}\tau_1&\tau_2&\tau_3\end{bmatrix}\begin{bmatrix}\dot{\theta}_1\\\dot{\theta}_2\\\dot{\theta}_3\end{bmatrix}&=\begin{bmatrix}F_{x}&F_{y}&F_{z}\end{bmatrix}\begin{bmatrix}\dot{x}_{p}\\\dot{y}_{p}\\\dot{z}_{p}\end{bmatrix}\\ \boldsymbol{\tau}^T\cdot\dot{\boldsymbol{\theta}}&=\boldsymbol{F}^T\cdot \boldsymbol{J}\cdot\dot{\boldsymbol{\theta}}\\ \end{aligned}$

则可以得到：

$\boldsymbol{\tau}=\boldsymbol{J}^T\cdot \boldsymbol{F}$

同样也可以通过关节力矩得到足端对地面的力

$\boldsymbol{F}=\boldsymbol{J}^{-T}\cdot \boldsymbol{\tau}$

地面对足端的力 $\boldsymbol{F}’=-\boldsymbol{F}$

四足运动学

改变姿态

目标：已知机身姿态，求关节角度

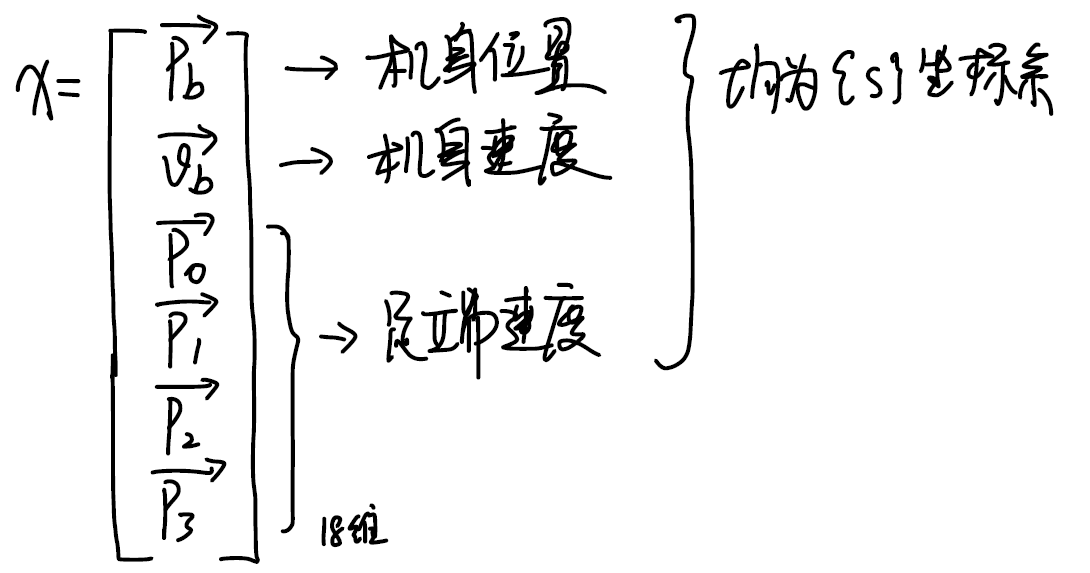
令足端静止在地面上，将右前腿 $P_0$ 点设为世界坐标系 $\{s\}$ 的原点，则 $\boldsymbol{p}_{si}$ 为常量

当 $\{s\}$ 和 $\{b\}$ 平行，此时 $\boldsymbol{R}_{sb}=\boldsymbol{I}$ ，可以得到四条腿相对于世界坐标系的位置：

$\begin{aligned} \boldsymbol{p}_{si}&=\boldsymbol{R}_{sb}\cdot[\boldsymbol{p}_{bi}(0)-\boldsymbol{p}_{b0}(0)]\\ &=\boldsymbol{I}\cdot[\boldsymbol{p}_{bi}(0)-\boldsymbol{p}_{b0}(0)]\\ &=\boldsymbol{p}_{bi}(0)-\boldsymbol{p}_{b0}(0) \end{aligned}$

在初始状态下，世界坐标系到机身坐标系的齐次变换矩阵为

$\boldsymbol{T}_{sb}(0)= \left[\begin{matrix}{\boldsymbol{R}_{sb}}&{\boldsymbol{O}_{s}}\\{\boldsymbol{0}_{1\times3}}&{1}\\\end{matrix}\right]= \left[\begin{matrix}{\boldsymbol{I}_{3}}&{-\boldsymbol{p}_{b0}(0)}\\{\boldsymbol{0}_{1\times3}}&{0}\\\end{matrix}\right]$

此时改变机身姿态，将其分解为平移与旋转 $\left\{
\begin{aligned}
\text{平移}&\quad p_d\\
\text{旋转}&\quad rpy(\alpha\beta\gamma)
\end{aligned}
\right.$

$\boldsymbol{T}_{sb}=\left[\begin{matrix}\boldsymbol{R}_{z}(\alpha)\boldsymbol{R}_{y}(\beta)\boldsymbol{R}_{x}(\gamma)&-\boldsymbol{p}_{b0}(0)+\boldsymbol{p}_{d}\\\boldsymbol{0}_{1\times3}&1\end{matrix}\right]$

即可求出机身坐标系下的足端坐标

$\boldsymbol{p}_{bi}=\boldsymbol{T}_{bs}\cdot \boldsymbol{p}_{si}=\boldsymbol{T}_{sb}^{-1}\cdot \boldsymbol{p}_{si}$

经过平移可以得到机器人单腿坐标系下的足端坐标，通过运动学逆解可以得到关节角度。

足端速度

足端速度由两方面叠加产生

关节转动产生的足端速度，利用雅可比矩阵可以求得： $\boldsymbol{v}_{bj}=\boldsymbol{J}\dot{\boldsymbol{\theta}}$
机身移动或旋转产生的足端速度： $\boldsymbol{v}_{be}$ ，此项待求

首先考虑刚体上一点的速度与加速度。在刚体平移或转动时，对于刚体上位置为 $\boldsymbol{p}$ 的质点$ P$ ，只考虑平移不考虑旋转，即只需要研究速度 $\dot{\boldsymbol{p}}$ 与加速度 $\ddot{\boldsymbol{p}}$ 。

设刚体在 $\{b\}$ 中的平移速度为 $\boldsymbol{v}_b$ 、旋转速度为 $\boldsymbol{\omega}_b$ ，即原点 $\boldsymbol{p}_O$ 的平移速度为 $\boldsymbol{v}_b$ 。刚体上位于 $\boldsymbol{p}_P$ 的质点以 $\boldsymbol{v}_b$ 平移，以 $\boldsymbol{\omega}_b$ 绕 $\boldsymbol{p}_O$ 旋转，则：

$\dot{\boldsymbol{p}}_P=\boldsymbol{v}_b+\boldsymbol{w}_b\times(\boldsymbol{p}_P-\boldsymbol{p}_O)=\boldsymbol{v}_b+[\boldsymbol{w}_b]_\times(\boldsymbol{p}_P-\boldsymbol{p}_O)$

对等式两边求导可得：

$\begin{aligned}\ddot{\boldsymbol{p}}_P&=\dot{\boldsymbol{v}}_b+[\dot{\boldsymbol{\omega}}_b]_\times(\boldsymbol{p}_P-\boldsymbol{p}_O)+[\boldsymbol{\omega}_b]_\times(\dot{\boldsymbol{p}}_P-\dot{\boldsymbol{p}}_O)\quad\text{其中 }\dot{\boldsymbol{p}}_O=\boldsymbol{v}_b\\&=\dot{\boldsymbol{v}}_b+[\boldsymbol{\omega}_b]_\times(\boldsymbol{p}_P-\boldsymbol{p}_O)+[\boldsymbol{\omega}_b]_\times[\boldsymbol{\omega}_b]_\times(\boldsymbol{p}_P-\boldsymbol{p}_O)\end{aligned}$

当前时刻原点与 $\{b\}$ 重合，$\boldsymbol{p}_O=\boldsymbol{0}$ ，则:

$\begin{aligned}\dot{\boldsymbol{p}}_P&=\boldsymbol{v}_b+[\boldsymbol{\omega}_b]_\times \boldsymbol{p}_P\\\ddot{\boldsymbol{p}}_P&=\dot{\boldsymbol{v}}_b+[\dot{\boldsymbol{\omega}}_b]_\times \boldsymbol{p}_P+[\boldsymbol{\omega}_b]_\times[\boldsymbol{\omega}_b]_\times \boldsymbol{p}_P\end{aligned} \tag{4}$

将机器人视为刚体，足端牵连速度为：（式中的bfB代表：{b}下feet2body）

$\boldsymbol{v}_{be}=\boldsymbol{v}_b+[\boldsymbol{\omega}_b]_\times \boldsymbol{p}_{bfB}$

结合开头的叠加， $\{s\}$ 下足端的速度可以表示为：

$\begin{aligned} \boldsymbol{v}_{sf} &=\boldsymbol{R}_{sb}\left(\boldsymbol{v}_{be}+\boldsymbol{v}_{bj}\right)\\ &=\boldsymbol{R}_{sb}\boldsymbol{v}_{b}+\boldsymbol{R}_{sb}[\boldsymbol{\omega}_{b}]_\times \boldsymbol{p}_{bfB}+J\dot{\theta})\\ &=\boldsymbol{v}_{s}+\boldsymbol{R}_{sb}([\boldsymbol{\omega}_{b}]_\times \boldsymbol{p}_{bfB}+J\dot{\theta}) \end{aligned}$

但式中的 $\boldsymbol{v}_s$ 无法测得。

$\{s\}$ 下足端相对于机身的速度可以表示为：

$\boldsymbol{v}_{sfB}=\boldsymbol{v}_{sf}-\boldsymbol{v}_{s}=\boldsymbol{R}_{sb}([\boldsymbol{\omega}_{b}]_\times \boldsymbol{p}_{bfB}+J\dot{\theta}) \tag{5}$

四足动力学

单刚体动力学

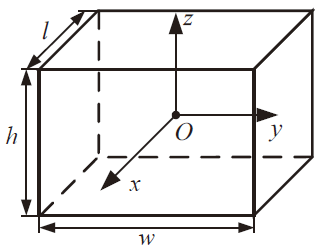
对于密度 $\rho(x,y,z)$ ，质量 $m=\int_z\int_y\int_x\rho(x,y,z)\mathrm{d}x\mathrm{d}y\mathrm{d}z=\int_B\rho\mathrm{d}V$ 的单刚体，将物体坐标系 $\{b\}$ 建在重心上，则 $\int_{B}\rho \boldsymbol{p}_{b}\mathrm{d}V=\boldsymbol{0}_{3\times1}$ ， $\int_{B}\rho [\boldsymbol{p}_{b}]\mathrm{d}V=\boldsymbol{0}_{3\times3}$ 。

根据牛二定律 $F=ma$ 与式 $(4)$ ，可以求出重心处所受的合外力 $\boldsymbol{f}_b$ ：

$\boldsymbol{f}_{b}=\int_{B}\rho \ddot{\boldsymbol{p}}_{b}\mathrm{d}V=\int_{B}\rho(\dot{\boldsymbol{v}}_{b}+[\dot{\boldsymbol{\omega}}_{b}]_\times \boldsymbol{p}_{b}+[\boldsymbol{\omega}_b]_\times[\boldsymbol{\omega}_b]_\times \boldsymbol{p}_{b})\mathrm{d}V$

提取常量 $\boldsymbol{v}_b$ 和 $\boldsymbol{\omega}_b$ ：

$\boldsymbol{f}_{b}=\dot{\boldsymbol{v}}_{b}\int_{B}\rho \mathrm{d}V+[\dot{\boldsymbol{\omega}}_{b}]_\times \int_{B}\rho \boldsymbol{p}_{b}dV+[\boldsymbol{\omega}_{b}]_\times [\boldsymbol{\omega}_{b}]_\times \int_{B}\rho \boldsymbol{p}_{b}\mathrm{d}V$

第一项中的 $\int_{B}\rho \mathrm{d}V=m$ ， $\int_{B}\rho \boldsymbol{p}_{b}dV=0$ ，则上式整理为：

$\boldsymbol{f}_b = m \dot{\boldsymbol{v}}_b \tag{6}$

计算重心处的合外力矩（力矩的计算公式为 $\boldsymbol{M}=\boldsymbol{p}\times \boldsymbol{f}$ ）：

$\begin{aligned} \boldsymbol{M}_b&=\int_{B}\left[\boldsymbol{p}_{b}\right]_\times\mathrm{d}\boldsymbol{f}=\int_{B}\left[\boldsymbol{p}_{b}\right]_\times\rho \ddot{\boldsymbol{p}}_{b}\mathrm{d}V\\ &= \underset{①}{\underline{\int_{B}\rho [\boldsymbol{p}_{b}]_\times\mathrm{d}V\cdot \dot{v}_{b}}}+ \underset{②}{\underline{\int_{B}\rho[\boldsymbol{p}_{b}]_\times[\dot{\boldsymbol{\omega}}_{b}]_\times \boldsymbol{p}_{b}\mathrm{d}V}}+ \underset{③}{\underline{\int_{B}\rho[\boldsymbol{p}_{b}]_\times[\boldsymbol{\omega}_b]_\times[\boldsymbol{\omega}_b]_\times \boldsymbol{p}_{b}\mathrm{d}V}} \end{aligned}$

分开看这三项：

对于式①：
$\int_{B}\rho [\boldsymbol{p}_{b}]_\times\mathrm{d}V=0$
对于式②：（ $\boldsymbol{a} \times \boldsymbol{b} = -\boldsymbol{b} \times \boldsymbol{a}$ ）
$\begin{aligned} \int_{B}\rho[\boldsymbol{p}_b]_\times[\dot{\boldsymbol{\omega}}_b]_\times \boldsymbol{p}_b\mathrm{d}V&=-\int_{B}\rho[\boldsymbol{p}_b]_\times[\boldsymbol{p}_b]_\times\dot{\boldsymbol{\omega}}_b\mathrm{d}V\\ &=\underline{\left(-\int_{B}\rho[\boldsymbol{p}_b]_\times[\boldsymbol{p}_b]_\times\mathrm{d}V\right)}\cdot\dot{\boldsymbol{\omega}}_b\\ &=\underline{\boldsymbol{I}_b}\dot{\boldsymbol{\omega}}_b \end{aligned}$
定义刚体惯性张量 $\boldsymbol{I}_b=-\int_{B}\rho[\boldsymbol{p}_b]_\times[\boldsymbol{p}_b]_\times\mathrm{d}V$
对于式③：（ $[\boldsymbol{a}]_\times[\boldsymbol{b}]_\times \boldsymbol{c}=(\boldsymbol{a}^{T}\boldsymbol{c})\boldsymbol{b}-(\boldsymbol{a}^{T}\boldsymbol{b})\boldsymbol{c}$ ， $\boldsymbol{a}\times \boldsymbol{a}=[\boldsymbol{a}]_\times \boldsymbol{a}=\boldsymbol{0}$ ）
$\begin{aligned}\int_{\mathcal{B}}\rho[\boldsymbol{p}_b]_\times[\boldsymbol{\omega}_b]_\times \boldsymbol{p}_b\mathrm{d}V&=\int_{\mathcal{B}}\rho[\boldsymbol{p}_b]_\times\left[(\boldsymbol{\omega}_b^T\boldsymbol{p}_b)\boldsymbol{\omega}_b-(\boldsymbol{\omega}_b^T\boldsymbol{\omega}_b)\boldsymbol{p}_b\right]\mathrm{d}V\\&=\int_{\mathcal{B}}\rho[(\boldsymbol{\omega}_b^T\boldsymbol{p}_b)[\boldsymbol{p}_b]_\times\boldsymbol{\omega}_b-(\boldsymbol{\omega}_b^T\boldsymbol{\omega}_b)[\boldsymbol{p}_b]_\times \boldsymbol{p}_b]\mathrm{d}V\\&=\int_{\mathcal{B}}\rho[(\boldsymbol{\omega}_b^T\boldsymbol{p}_b)[\boldsymbol{p}_b]_\times\boldsymbol{\omega}_b-\boldsymbol{0}]\mathrm{d}V\\&=-\int_{\mathcal{B}}\rho[(\boldsymbol{\omega}_b^T\boldsymbol{p}_b)[\boldsymbol{\omega}_b]_\times \boldsymbol{p}_b-\boldsymbol{0}]\mathrm{d}V\\ &=-\int_B\rho[(\boldsymbol{\omega}_b+\boldsymbol{p}_b)[\boldsymbol{\omega}_b]_\times \boldsymbol{p}_b-(\boldsymbol{p}_b^T\boldsymbol{p}_b)[\boldsymbol{\omega}_b]_\times \boldsymbol{\omega}_b]\mathrm{d}V\\&=-\int_B\rho[\boldsymbol{\omega}_b]_\times[(\boldsymbol{\omega}_b^T\boldsymbol{p}_b)\boldsymbol{p}_b-(\boldsymbol{p}_b^T\boldsymbol{p}_b)\boldsymbol{\omega}_b]\mathrm{d}V\\ &=-\int_{B}\rho[\boldsymbol{\omega}_b]_\times[\boldsymbol{p}_b]_\times[\boldsymbol{p}_b]_\times\boldsymbol{\omega}_b\mathrm{d}V\\&=[\boldsymbol{\omega}_b]_\times\left(\underline{-\int_{B}\rho[\boldsymbol{p}_b]_\times[\boldsymbol{p}_b]_\times\mathrm{d}V}\right)\boldsymbol{\omega}_b\\&=[\boldsymbol{\omega}_b]_\times\underline{\boldsymbol{I}_{b}}\boldsymbol{\omega}_b \end{aligned}$
倒数第二项的下划线部分即为惯性张量。

综上可以得到旋转刚体的欧拉方程：

$M_b=\boldsymbol{I}_{b}\dot{\boldsymbol{\omega}}_{b}+[\boldsymbol{\omega}_{b}]_\times \boldsymbol{I}_{b}\boldsymbol{\omega}_{b} \tag{7}$

上式中的惯性张量：

$\begin{aligned} \boldsymbol{I}_{b}& =-\int_{B}\rho[\boldsymbol{p}_{b}]_\times[\boldsymbol{p}_{b}]_\times\mathrm{d}V \\ &=-\int_{B}\rho\left[\begin{matrix}{0}&{-p_{z}}&{p_{y}}\\{p_{z}}&{0}&{-p_{x}}\\{-p_{y}}&{p_{x}}&{0}\\\end{matrix}\right]\left[\begin{matrix}{0}&{-p_{z}}&{p_{y}}\\{p_{z}}&{0}&{-p_{x}}\\{-p_{y}}&{p_{x}}&{0}\\\end{matrix}\right]\mathrm{d}V \\ &=\int_{B}\rho\left[\begin{matrix}{p_{y}^{2}+p_{z}^{2}}&{-p_{x}p_{y}}&{-p_{x}p_{z}}\\{-p_{x}p_{y}}&{p_{x}^{2}+p_{z}^{2}}&{-p_{y}p_{z}}\\{-p_{x}p_{z}}&{-p_{y}p_{z}}&{p_{x}^{2}+p_{y}^{2}}\\\end{matrix}\right]\mathrm{d}V \\ &=\begin{bmatrix}I_{xx}&I_{xy}&I_{xz}\\I_{xy}&I_{yy}&I_{yz}\\I_{xz}&I_{yz}&I_{zz}\end{bmatrix} \end{aligned}$

即可以得到下面的结论。可以计算形状不规则、密度不均匀的物体。

$\begin{cases} \boldsymbol{I}_{xx}=\int_{B}\rho\left(p_y^2+p_z^2\right)\mathrm{d}V\\ \boldsymbol{I}_{yy}=\int_{B}\rho\left(p_x^2+p_z^2\right)\mathrm{d}V\\ \boldsymbol{I}_{zz}=\int_{B}\rho\left(p_x^2+p_y^2\right)\mathrm{d}V\\ \boldsymbol{I}_{xy}=-\int_{B}\rho p_xp_y\mathrm{d}V\\ \boldsymbol{I}_{xz}=-\int_{B}\rho p_xp_z\mathrm{d}V\\ \boldsymbol{I}_{yz}=-\int_{B}\rho p_yp_z\mathrm{d}V \end{cases}$

例如对于长方体：

$\boldsymbol{I}_b=\frac1{12}\begin{bmatrix}m(\omega^2+h^2)&0&0\\0&m(l^2+h^2)&0\\0&0&m(l^2+\omega^2)\end{bmatrix}$

在机身坐标系中， $\boldsymbol{I}_b$ 为常量（只与形状、密度分布有关），刚体旋转后世界坐标系下的 $\boldsymbol{I}_s$ 会改变。

单刚体动能

由式 $(4)$ ，可以得到刚体整体的动能：（ $v_x^2+v_y^2+v_z^2=\boldsymbol{v}^T\boldsymbol{v}$ ）

$\begin{aligned}K&=\int_B\frac{1}{2}\rho \boldsymbol{v}^T\boldsymbol{v}\mathrm{d}V\\&=\frac12\int_B\rho(\boldsymbol{v}_b+[\boldsymbol{\omega}_b]_\times \boldsymbol{p}_b)^T(\boldsymbol{v}_b+[\boldsymbol{\omega}_b]_\times \boldsymbol{p}_b)\mathrm{d}V\\&=\frac12\int_B\rho(\boldsymbol{v}_b^T+\boldsymbol{p}_b^T[\boldsymbol{\omega}_b]_\times^T)\left(\boldsymbol{v}_b+[\boldsymbol{\omega}_b]_\times \boldsymbol{p}_b\right)\mathrm{d}V\\ &= \underset{①}{\underline{\frac12\int_B\rho \underset{与\boldsymbol{v}_b有关}{\underline{\boldsymbol{v}_b^T\boldsymbol{v}_b}}\mathrm{d}V}}+ \underset{②}{\underline{\frac12\boldsymbol{v}_b^T[\boldsymbol{\omega}_b]_\times\underset{0}{\underline{\int _B\rho \boldsymbol{p}_b\mathrm{d}V}}}}+ \underset{③}{\underline{\frac12\underset{0}{\underline{\int_B\rho \boldsymbol{p}_b^T\mathrm{d}V}}[\boldsymbol{\omega}_b]_\times^T\boldsymbol{v}_b}}+ \underset{④}{\underline{\frac12\int_B\rho \boldsymbol{p}_b^T\underset{与\boldsymbol{\omega}_b有关}{\underline{[\boldsymbol{\omega}_b]_\times^T[\boldsymbol{\omega}_b]_\times}}\boldsymbol{p}_b\mathrm{d}V}}\end{aligned}$

分开看这四项：

式②、③为0
式①与 $\boldsymbol{v}_b$ 有关，定义为移动动能 $K_m$
$\begin{aligned} K_{m}=& \frac{1}{2}\int_{B}\rho \boldsymbol{v}_{b}^{\mathrm{T}}\boldsymbol{v}_{b}\:\mathrm{d}V \\ =& \frac{1}{2}\int_{B}\rho\:\mathrm{d}V\boldsymbol{v}_{b}^{\mathrm{T}}\boldsymbol{v}_{b} \\ =& \frac{1}{2}m\boldsymbol{v}_{b}^{\mathrm{T}}\boldsymbol{v}_{b} \end{aligned}$
式③与 $\boldsymbol{\omega}_b$ 有关，定义为转动动能 $K_t$
$\begin{aligned} K_t&=\frac12\int_B\rho \boldsymbol{p}_b^T[\boldsymbol{\omega}_b]_\times^T[\boldsymbol{\omega}_b]_\times \boldsymbol{p}_b\mathrm{d}V\\&=-\frac12\int_B\rho \boldsymbol{p}_b^T[\boldsymbol{\omega}_b]_\times[\boldsymbol{\omega}_b]_\times \boldsymbol{p}_b\mathrm{d}V\\ &=-\frac{1}{2}\int_{B}\rho \boldsymbol{p}_{b}^{T}[(\boldsymbol{\omega}_{b}^{T}\boldsymbol{p}_{b})\boldsymbol{\omega}_{b}-(\boldsymbol{\omega}_{b}^{T}\boldsymbol{\omega}_{b})\boldsymbol{p}_{b}]dV \\ &=-\frac{1}{2}\int_{B}\rho [(\boldsymbol{\omega}_{b}^{T}\boldsymbol{p}_{b})(\boldsymbol{p}_{b}^{T}\boldsymbol{\omega}_{b})-(\boldsymbol{\omega}_{b}^{T}\boldsymbol{\omega}_{b})(\boldsymbol{p}_{b}^{T}\boldsymbol{p}_{b})]dV \\ &=-\frac{1}{2}\int_{B}\rho [(\boldsymbol{p}_{b}^{T}\boldsymbol{\omega}_{b})(\boldsymbol{\omega}_{b}^{T}\boldsymbol{p}_{b})-(\boldsymbol{p}_{b}^{T}\boldsymbol{p}_{b})(\boldsymbol{\omega}_{b}^{T}\boldsymbol{\omega}_{b})]dV \\ &=-\frac{1}{2}\int_{B}\rho \boldsymbol{\omega}_{b}^{T}\left[(\boldsymbol{p}_{b}^{T}\boldsymbol{\omega}_{b})\boldsymbol{p}_{b}-(\boldsymbol{p}_{b}^{T}\boldsymbol{p}_{b})\boldsymbol{\omega}_{b}\right]dV \\ &=\frac{1}{2}\boldsymbol{\omega}_{b}^{T}\int_{B}-\rho[\boldsymbol{p}_{b}]_\times[\boldsymbol{p}_{b}]_\times\boldsymbol{\omega}_{b}dV \\ &=\frac{1}{2}\boldsymbol{\omega}_b^{T}\boldsymbol{I}_{b}\boldsymbol{\omega}_b \end{aligned}$
在不同坐标系下，刚体的转动动能 $K_t$ 相等。又由 $\boldsymbol{\omega}_{b}=\boldsymbol{R}_{bs}\boldsymbol{\omega}_{s}$ ，故：
$\begin{aligned} K_{st}& =K_{bt} \\ \frac{1}{2}\boldsymbol{\omega}_{s}^{\mathrm{T}}\boldsymbol{I}_{s}\boldsymbol{\omega}_{s}& =\frac12\boldsymbol{\omega}_b^\mathrm{T}\boldsymbol{I}_b\boldsymbol{\omega}_b \\ \boldsymbol{\omega}_{s}^{\mathrm{T}}\boldsymbol{I}_{s}\boldsymbol{\omega}_{s}& =(\boldsymbol{R}_{bs}\boldsymbol{\omega}_{s})^{\mathrm{T}}\boldsymbol{I}_{b}(\boldsymbol{R}_{bs}\boldsymbol{\omega}_{s}) \\ \boldsymbol{\omega}_{s}^{\mathrm{T}}\boldsymbol{I}_{s}\boldsymbol{\omega}_{s}& =\boldsymbol{\omega}_{s}^{\mathrm{T}}(\boldsymbol{R}_{sb}\boldsymbol{I}_{b}\boldsymbol{R}_{sb}^{\mathrm{T}})\boldsymbol{\omega}_{s} \\ \boldsymbol{I}_{s}&=\boldsymbol{R}_{sb}\boldsymbol{I}_{b}\boldsymbol{R}_{sb}^\mathrm{T} \end{aligned}$
由此可以得到世界坐标系下刚体的惯性张量，这将在下一节中被用到。

四足动力学

目标：找到足端力与机器人运动的联系。

由式 $(6)$ 和 $(7)$ 可以得到：

$\begin{cases} \boldsymbol{f}_b=m\dot{\boldsymbol{v}}_b\\ \boldsymbol{M}_b=\boldsymbol{I}_b\dot{\boldsymbol{\omega}}_b+\underline{[\boldsymbol{\omega}_b]_\times \boldsymbol{I}_b\boldsymbol{\omega}_b} \end{cases}$

由于四足机器人运动时一般不会快速旋转，上式中 $\boldsymbol{\omega}_b$ 很小，故划线部分可以忽略。则上式变为：

$\begin{cases} \boldsymbol{f}_b=m\dot{\boldsymbol{v}}_b\\ \boldsymbol{M}_b=\boldsymbol{I}_b\dot{\boldsymbol{\omega}}_b \end{cases}$

在世界坐标系中同样满足上式，即为：

$\begin{cases} \boldsymbol{f}_s=m\dot{\boldsymbol{v}}_s\\ \boldsymbol{M}_s=\boldsymbol{I}_s\dot{\boldsymbol{\omega}}_s=\boldsymbol{R}_\mathrm{sb}\boldsymbol{I}_{b}\boldsymbol{R}_\mathrm{sb}^\mathrm{T}\dot{\boldsymbol{\omega}}_s \end{cases}$

其中，合外力 $\boldsymbol{f}_s$ 由两部分组成：

重力 $mg$
足端力 $\boldsymbol{f}_{is}$

合力矩 $\boldsymbol{M}_s$ 由两部分组成：

重力穿过重心，力矩为 $0$
足端力对重心的力矩 $\boldsymbol{p}_{gi}\times \boldsymbol{f}_{is} = [\boldsymbol{p}_{gi}]\boldsymbol{f}_{is}$

则：

$\left\{ \begin{aligned} &mg+\sum_{i=0}^3\boldsymbol{f}_{is}=m\dot{\boldsymbol{v}}_s\\ &\sum_{i=0}^3[\boldsymbol{p}_{ig}]_\times \boldsymbol{f}_{is}=\boldsymbol{R}_{sb}\boldsymbol{I}_b\boldsymbol{R}_{sb}^\mathrm{T}\dot{\boldsymbol{\omega}}_s \end{aligned} \right. \tag{8}$

整理成矩阵形式

$\begin{bmatrix} \boldsymbol{I}&\boldsymbol{I}&\boldsymbol{I}&\boldsymbol{I}\\ [\boldsymbol{p}_{g0}]_\times&[\boldsymbol{p}_{g1}]_\times&[\boldsymbol{p}_{g2}]_\times&[\boldsymbol{p}_{g3}]_\times\end{bmatrix}\begin{bmatrix}\boldsymbol{f}_{s0}\\\boldsymbol{f}_{s1}\\\boldsymbol{f}_{s2}\\\boldsymbol{f}_{s3}\end{bmatrix}=\begin{bmatrix}m(\dot{\boldsymbol{v}}_s-g)\\\boldsymbol{R}_{sb}\boldsymbol{I}_b\boldsymbol{R}_{sb}^\mathrm{T}\dot{\boldsymbol{\omega}}_s \end{bmatrix}$

此时完成了足端力与机器人运动的联系。但此时无法获得机器人姿态 $\boldsymbol{R}_{sb}$ ，且需要知道机器人在世界坐标系下的 $\boldsymbol{v}_s$ 、 $\boldsymbol{\omega}_s$ 。获取这些信息需要用到下一章的状态估计器。

状态估计器

状态估计器是四足机器人系统中比较重要的一环节，通过状态估计器可以获得四足机器人质心位姿（位置和姿态角）及速度。姿态角可根据IMU通过坐标变换得到；位置和速度需要使用最小二乘法或卡尔曼滤波器求得，最终将质心位姿和速度作为机械狗的MPC+WBC控制器及单刚体动力学的反馈输入，进而形成了整个系统的闭环控制。本章节分别介绍最小二乘估计和离散卡尔曼滤波器这两个优化方法。

最小二乘与卡尔曼滤波

在讲状态估计器之前有必要介绍一下最小二乘和卡尔曼滤波的关系。线性回归是一类问题的概念，而最小二乘估计、最小均方误差估计是参数估计方法，最小二乘法、Kalman、梯度下降都是参数优化方法。最小二乘是优化方法中的一种特殊情况，卡尔曼滤波是最小二乘法的一种特殊情况。 古典最小二乘中，假设了每一次测量的权重相同，但事实上这样并不合理，后来演化为加权最小二乘法，至此最小二乘估计所做的都是批处理（Batch），这样比较占内存，不符合动态系统状态估计的需要，即每一次更新输入时，都要从新计算之前所有的记录值。而后，提出递推最小二乘法，模型就不用每次都重新计算了。与递归最小二乘相似，卡尔曼滤波加入了系统内部变化的考虑。即利用process model对系统在下一时刻的状态进行预测。当对于系统不够了解时，使用最小二乘法比较合适，而对于系统了解比较多时，可以采用Kalman滤波。改变量测噪声、系统噪声都会对Kalman滤波的效果产生影响，而不会对最小二乘滤波产生影响，而改变最小二乘的阶数会对其产生影响。

使用IMU获得姿态

使用IMU可以估计质心姿态。现有的IMU基本都可以返回四元数 $\boldsymbol{q}=\begin{bmatrix}w\\x\\y\\z\end{bmatrix}$ ，经过计算即可获得质心姿态角，其公式如下：

$\boldsymbol{R}_{sb} = \begin{bmatrix} 1-2 y^{2}-2 z^{2} & 2 x y-2 z w & 2 x z+2 y w \\ 2 x y+2 z w & 1-2 x^{2}-2 z^{2} & 2 y z-2 x w \\ 2 x z-2 y w & 2 y z+2 x w & 1-2 x^{2}-2 y^{2} \end{bmatrix}$

当然，也可以通过旋转矩阵转成欧拉角（Roll、Pitch、Yaw）：

$\begin{aligned} \text{Roll} &= \arctan2\left(\boldsymbol{R}_{sb}(3,2), \boldsymbol{R}_{sb}(3,3)\right) \\ \text{Pitch} &= \arcsin\left(-\boldsymbol{R}_{sb}(3,1)\right) \\ \text{Yaw} &= \arctan2\left(\boldsymbol{R}_{sb}(2,1), \boldsymbol{R}_{sb}(1,1)\right) \end{aligned}$

在IMU的局部坐标系 $\{b\}$ 中：

$\begin{aligned}m\boldsymbol{a}&=-k\boldsymbol{s}+m\boldsymbol{R}_{bs}\boldsymbol{g}\\\boldsymbol{s}&=\frac{m}{k}(\boldsymbol{R}_{bs}\boldsymbol{g}-\boldsymbol{a})\end{aligned}$

上式中由于重力加速度 $\boldsymbol{g}=\begin{bmatrix}0\\ 0 \-9.8\end{bmatrix}$ 是世界坐标系下的，所以需要左乘旋转矩阵 $\boldsymbol{R}_{bs}$ 。则加速度计的读数为：

$\begin{aligned}\boldsymbol{a}_b=\boldsymbol{a}_{out}=-\frac{k}{m}\boldsymbol{s}&=\boldsymbol{a}-\boldsymbol{R}_{bs}\boldsymbol{g}=\boldsymbol{a}-\boldsymbol{R}_{sb}^\mathrm{T}\boldsymbol{g}\end{aligned}$

上述公式建立了加速度计读数与质心姿态的关系，通过左乘旋转矩阵可以计算出IMU在 $\{s\}$ 坐标系下的加速度：

$\begin{aligned} \boldsymbol{a}_{s}& =\boldsymbol{R}_{sb}\boldsymbol{a} \\ &=\boldsymbol{R}_{sb}\boldsymbol{a}_{b}+\boldsymbol{R}_{sb}\boldsymbol{R}_{sb}^{T}\boldsymbol{g} \\ &=\boldsymbol{R}_{sb}\boldsymbol{a}_{b}+\boldsymbol{g} \end{aligned} \tag{9}$

状态空间模型

状态估计器需要一个描述四足机器人运动状态的状态空间模型。对于一个状态空间模型需要对其进行能控性和能观性的分析，来判断此学系统是否能够被输入所控制，但本文省略这一部分的内容。本章节先介绍连续状态空间模型，再推出离散状态空间模型。

连续状态空间模型

“连续”指的是时间连续、定常线性系统的状态空间模型：

$\begin{cases}\dot{\boldsymbol{x}}(t)=\boldsymbol{A}_c \boldsymbol{x}(t)+\boldsymbol{B}_c \boldsymbol{u}(t)\\ \boldsymbol{y}(t)=\boldsymbol{C}_c \boldsymbol{x}(t)\end{cases} \tag{10}$

其中：

$\boldsymbol{x}(t)$ ：状态向量
$\boldsymbol{u}(t)$ ：控制向量
$\boldsymbol{y}(t)$ ：输出向量
$\boldsymbol{A}_c$ ：系统矩阵
$\boldsymbol{B}_c$ ：输入矩阵
$\boldsymbol{C}_c$ ：输出矩阵

则 $\boldsymbol{x}$ 应为要估计的量， $\boldsymbol{y}$ 为能直接测量的量。

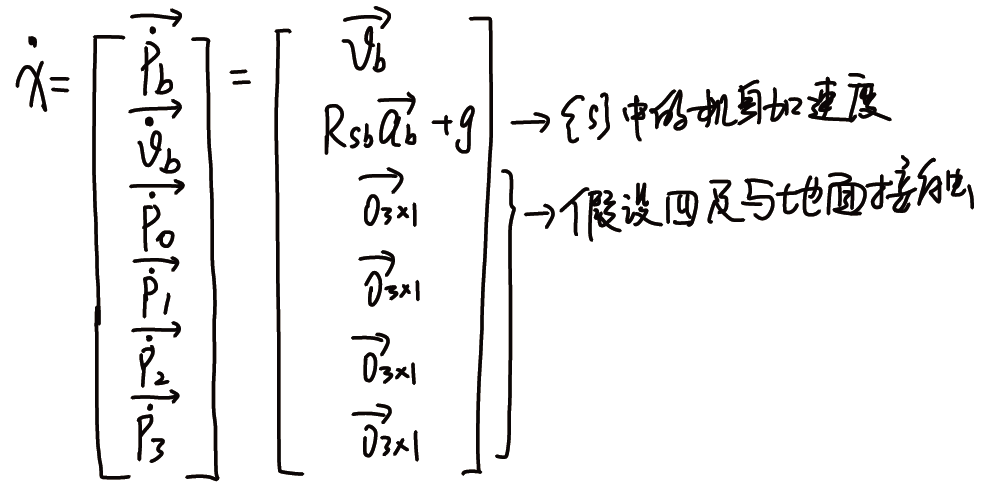
令机身加速度 $\boldsymbol{a}_s$ 为系统输入量 $\boldsymbol{u}$ ，上式可变为标准形式：

$\dot{\boldsymbol{x}}= \begin{bmatrix} \boldsymbol{0}_{3\times3}&\boldsymbol{I}_3&\boldsymbol{0}_{3\times12}\\ &\boldsymbol{0}_{3\times18}&\\ &\boldsymbol{0}_{3\times18}& \end{bmatrix}\boldsymbol{x}+ \begin{bmatrix}\boldsymbol{0}_{3\times3}\\\boldsymbol{I}_3\\\boldsymbol{0}_{3\times3} \end{bmatrix} \begin{bmatrix}\boldsymbol{R}_{sb}\boldsymbol{a}_{b}+\boldsymbol{g}\end{bmatrix} \tag{11}$

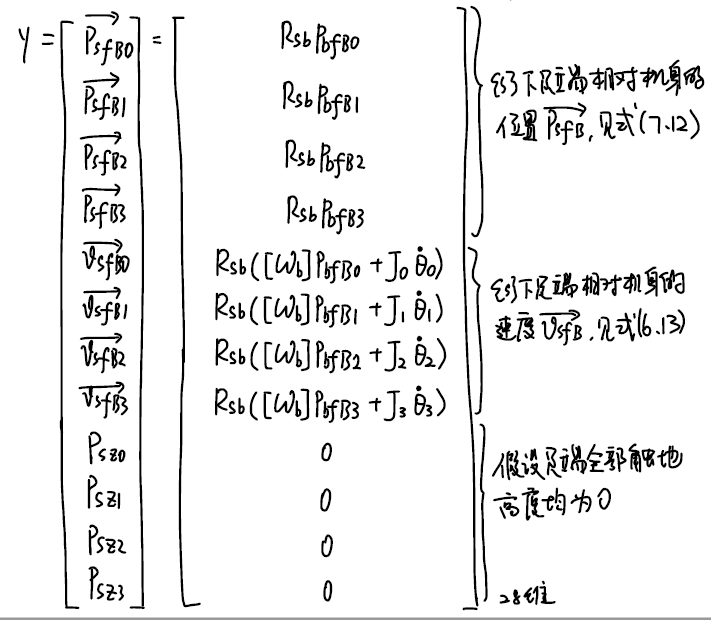
对于可测量的输出变量 $\boldsymbol{y}$ ，前文通过IMU可测得 $\{s\}$ 坐标系下的机身姿态 $\boldsymbol{R}_{sb}$ ； $\{b\}$ 下的加速度 $\boldsymbol{a_b}$ 、角速度 $\boldsymbol{\omega}_b$ ；通过正向运动学，可以求出 $\{b\}$ 坐标系下足端相对于机身的位置 $\boldsymbol{p}_{bfB}$ ，转换到 $\{s\}$ 坐标系下，即 $\boldsymbol{p}_{sfB}=\boldsymbol{R}_{sb}\boldsymbol{p}_{bfB}$ (式12)，即可写出输出变量：

将其写成式 $(10)$ 的标准形式：(式13)

离散状态空间模型

由于控制算法运行于计算机，需要对连续的状态空间模型离散化，使状态空间变量均为时间的函数。设采样时间间隔为 $\mathrm{d}t$ ，则：

$\dot{\boldsymbol{x}}(k-1)=\frac{\boldsymbol{x}(k)-\boldsymbol{x}(k-1)}{dt}\Rightarrow \boldsymbol{x}(k)=\boldsymbol{x}(k-1)+\mathrm{d}t\dot{\boldsymbol{x}}(k-1)$

将式 $(10)$ 带入

$\begin{aligned} \boldsymbol{x}(k)&=\boldsymbol{x}(k-1)+\mathrm{d}t\left(\boldsymbol{A}_{c}\boldsymbol{x}(k-1)+\boldsymbol{B}_{c}\boldsymbol{u}(k-1)\right)\\ &=\underline{(\boldsymbol{I}+\mathrm{d}t\boldsymbol{A}_{c})}\boldsymbol{x}(k-1)+\underline{\mathrm{d}t\boldsymbol{B}_{c}}\boldsymbol{u}(k-1) \end{aligned}$

则离散状态空间模型可以表示为：

$\begin{aligned} \begin{cases}\boldsymbol{x}(k)=\boldsymbol{A}\boldsymbol{x}(k-1)+\boldsymbol{B}\boldsymbol{u}(k-1)\\\boldsymbol{y}(k)=\boldsymbol{C}\boldsymbol{x}(k)\end{cases} \quad\text{其中}\begin{cases}\boldsymbol{A}=\boldsymbol{I}+\mathrm{d}t\boldsymbol{A}_{c}\\\boldsymbol{B}=\mathrm{d}t\boldsymbol{B}_{c}\\\boldsymbol{C}=\boldsymbol{C}_{c}\end{cases} \end{aligned}$

最小二乘估计

输出向量 $\boldsymbol{y}$ 的测量值中含有噪声向量 $\boldsymbol{v}$ ，假设状态向量 $\boldsymbol{x}_k$ 为定值 $\boldsymbol{x}$ ，离散状态空间中的 $\boldsymbol{y}$ 变为 $\boldsymbol{y}_k=\boldsymbol{C}\boldsymbol{x}+\boldsymbol{v}_k$ 。假设测量噪声 $\boldsymbol{v}\sim(0,\boldsymbol{R})$ ，其中 $\boldsymbol{R}$ 为协方差矩阵， $\boldsymbol{R}=\mathrm{diag}(\sigma_{1}^{2},\sigma_{2}^{2},\ldots,\sigma_{n}^{2})$ 。需要在有噪声的情况下获得状态向量的最优估计值 $\hat{\boldsymbol{x}}$ 。

加权最小二乘估计

定义测量残差 $\boldsymbol{\epsilon}_{y}=\boldsymbol{y}-\boldsymbol{C}\hat{\boldsymbol{x}}$ 。根据各个传感器的误差方差定义为权重，方差越小权重越大。定义代价函数：

$\begin{aligned} J&= \frac{\boldsymbol{\epsilon}_{y_{1}}^{2}}{\sigma_{1}^{2}}+ \frac{\boldsymbol{\epsilon}_{y_{2}}^{2}}{\sigma_{2}^{2}}+ \cdots+ \frac{\boldsymbol{\epsilon}_{y_{n}}^{2}}{\sigma_{n}^{2}}=\boldsymbol{\epsilon}_{y}^{T}\boldsymbol{R}^{-1}\boldsymbol{\epsilon}_{y}\\ &=(\boldsymbol{y}-\boldsymbol{C}\hat{\boldsymbol{x}})^{T}\boldsymbol{R}^{-1}(\boldsymbol{y}-\boldsymbol{C}\hat{\boldsymbol{x}})\\ &=\boldsymbol{y}^{T}\boldsymbol{R}^{-1}\boldsymbol{y}-\boldsymbol{y}^{T}\boldsymbol{R}^{-1}\boldsymbol{C}\hat{\boldsymbol{x}}-\hat{\boldsymbol{x}}^{T}\boldsymbol{C}^{T}\boldsymbol{R}^{-1}\boldsymbol{y}+\hat{\boldsymbol{x}}^{T}\boldsymbol{C}^{T}\boldsymbol{R}^{-1}\boldsymbol{C}\hat{\boldsymbol{x}}\\ \end{aligned}$

求 $J$ 的偏导数 $\frac{\partial J}{\partial\hat{\boldsymbol{x}}}=-2\boldsymbol{y}^{T}\boldsymbol{R}^{-1}\boldsymbol{C}+2\hat{\boldsymbol{x}}^{T}\boldsymbol{C}^{T}\boldsymbol{R}^{-1}\boldsymbol{C}$ ，令其为 $0$ ，可以计算出 $\hat{\boldsymbol{x}}=(\boldsymbol{C}^{T}\boldsymbol{R}^{-1}\boldsymbol{C})^{-1}\boldsymbol{C}^{T}\boldsymbol{R}^{-1}\boldsymbol{y}$ 。

但此方法需要使用一段时间内所有的测量值 $\boldsymbol{y}$ ，其计算量及内存占用太大，故改用递推公式。

递推最小二乘估计

定义 $\hat{\boldsymbol{x}}$ 的递推公式：（其中 $\boldsymbol{K}_k$ 为最优修正系数矩阵）

$\begin{cases} \boldsymbol{y}_{k}=\boldsymbol{C}\boldsymbol{x}+\boldsymbol{v}_{k}\\ \hat{\boldsymbol{x}}_{k}=\hat{\boldsymbol{x}}_{k-1}+\boldsymbol{K}_{k}(\boldsymbol{y}_{k}-\boldsymbol{C}\hat{\boldsymbol{x}}_{k-1}) \end{cases} \tag{13}$

定义 $k$ 时刻的状态估计误差：

$\begin{aligned} \boldsymbol{\omega}_k&=\hat{\boldsymbol{x}}-\hat{\boldsymbol{x}}_k=\hat{\boldsymbol{x}}-\hat{\boldsymbol{x}}_{k-1}-\boldsymbol{K}_k(\boldsymbol{y}_k-\boldsymbol{C}\hat{\boldsymbol{x}}_{k-1})\\ &=\boldsymbol{\omega}_{k-1}-\boldsymbol{K}_k\boldsymbol{C}(\boldsymbol{x}-\hat{\boldsymbol{x}}_{k-1})-\boldsymbol{K}_k\boldsymbol{v}_k\\ &=(\boldsymbol{I}-\boldsymbol{K}_k\boldsymbol{C})\boldsymbol{\omega}_{k-1}-\boldsymbol{K}_k\boldsymbol{v}_k \end{aligned} \tag{14}$

再次使用二次规划，令 $k$ 时刻各状态估计误差方差和最小，则 $k$ 时刻的代价函数 $J_k$ 为：

$\begin{aligned}J_{k}&=E\left(\omega_{k1}^{2}+\omega_{k2}^{2}+\cdots+\omega_{kn}^{2}\right)\\&=\sigma_{k1}^{2}+\sigma_{k2}^{2}+\cdots+\sigma_{kn}^{2}\\&=\mathrm{Tr}\left(\boldsymbol{P}_{k}\right)\end{aligned}$

估计误差协方差 $\boldsymbol{P}_{k}=E(\boldsymbol{\omega}_{k}\boldsymbol{\omega}_{k}^{T})$ ，将式 $(14)$ 带入可以得到：

$\begin{aligned} \boldsymbol{P}_{k}&=E(\boldsymbol{\omega}_{k}\boldsymbol{\omega}_{k}^{T})\\ &=(\boldsymbol{I}-\boldsymbol{K}_k\boldsymbol{C})\boldsymbol{P}_{k-1}(\boldsymbol{I}-\boldsymbol{K}_k\boldsymbol{C})^T+\boldsymbol{K}_k\boldsymbol{R}\boldsymbol{K}_k^T \end{aligned} \tag{15}$

目的为使 $J$ 最小，对其求偏导：

$\frac{\partial J_k}{\partial \boldsymbol{K}_k}=2(\boldsymbol{I}-\boldsymbol{K}_k \boldsymbol{C})\boldsymbol{P}_{k-1}(-\boldsymbol{C}^T)+2\boldsymbol{K}_k \boldsymbol{R}=0$

解得最优的 $\boldsymbol{K}_k$ 为：

$\boldsymbol{K}_{k}=\boldsymbol{P}_{k-1}\boldsymbol{C}^{T}(\boldsymbol{R}+\boldsymbol{C}\boldsymbol{P}_{k-1}\boldsymbol{C}^{T})^{-1} \tag{16}$

最小二乘估计流程总结

确定初始状态的最优估计值 $\hat{\boldsymbol{x}}_0$ 和估计值的协方差 $\boldsymbol{P}_0$ 。如果对系统状态 $\boldsymbol{x}$ 完全不了解，则可以将 $\hat{\boldsymbol{x}}_0$ 设为任意值，同时令 $\boldsymbol{P}_0 = \infty \boldsymbol{I}$ ，表示无穷大的协方差，即完全不信任 $\hat{\boldsymbol{x}}_0$ 。
估计器运行开始，在 $k=1$ 时刻，机器人从各个传感器得到输出向量 $\boldsymbol{y}_1$ ，并根据式 $(16)$ 计算出当前时刻的最优修正系数矩阵 $\boldsymbol{K}_1=\boldsymbol{P}_0\boldsymbol{C}^{T}(\boldsymbol{R}+\boldsymbol{C}\boldsymbol{P}_0\boldsymbol{C}^{T})^{-1}$ 。根据式 $(13)$ 可以计算出当前时刻的最优估计值 $\hat{\boldsymbol{x}}_1=\hat{\boldsymbol{x}}_0+\boldsymbol{K}_1(\boldsymbol{y}_1-\boldsymbol{C}\hat{\boldsymbol{x}}_0)$ 。根据式 $(15)$ 可以计算出估计误差协方差 $\boldsymbol{P}_1=(\boldsymbol{I}-\boldsymbol{K}_1\boldsymbol{C})\boldsymbol{P}_0(\boldsymbol{I}-\boldsymbol{K}_1\boldsymbol{C})^T+\boldsymbol{K}_1\boldsymbol{R}\boldsymbol{K}_1^T$ 。
当 $k=2,3,\cdots $ ，估计器重复第二步，估计值 $\hat{\boldsymbol{x}}$ 不断逼近真实状态 $\boldsymbol{x}$ 。

过程噪声

前文假设状态向量为定值。若状态向量是变化的，增加过程噪声 $\boldsymbol{w}$ ，且其期望为0。则离散状态空间模型变为：

$\boldsymbol{x}_k=\boldsymbol{A}\boldsymbol{x}_{k-1}+\boldsymbol{B}\boldsymbol{u}_{k-1}+\boldsymbol{w}$

状态期望为：

$\begin{aligned} \overline{\boldsymbol{x}_{k}} &=E(\boldsymbol{x}_{k})=\boldsymbol{A}E(\boldsymbol{x}_{k-1})+\boldsymbol{B}E(\boldsymbol{u}_{k-1})+\underset{0}{\underline{E(\boldsymbol{w}_{k-1}}})\\ &=\boldsymbol{A}\overline{\boldsymbol{x}}_{k-1}+\boldsymbol{B}\overline{\boldsymbol{u}}_{k-1} \end{aligned}$

状态向量 $\boldsymbol{x}_k$ 的协方差为：（ $\boldsymbol{Q}=\boldsymbol{w}\boldsymbol{w}^T$ 为过程噪声协方差）

$\begin{aligned} P_k &=E\left[(\boldsymbol{x}_k-\overline{\boldsymbol{x}}_k)(\boldsymbol{x}_k-\overline{\boldsymbol{x}}_k)^T\right]=\boldsymbol{A}\boldsymbol{P}_{k-1}\boldsymbol{A}^T+\boldsymbol{w}_{k-1}\boldsymbol{w}_{k-1}^T\\ &=\boldsymbol{A}\boldsymbol{P}_{k-1}\boldsymbol{A}^T+\underline{\boldsymbol{Q}} \end{aligned}$

扩展卡尔曼滤波器

最小二乘估计只能对固定状态 $\boldsymbol{x}$ 进行估计，而扩展卡尔曼滤波器可以对变化的状态 $\boldsymbol{x}_k$ 进行估计。

TODO

步态轨迹规划

落脚点的选取

平移

TODO 图

上图为四足机器人的一条腿从抬起到落下的过程，分区看图中的几个过程：

➂为中性落脚点
➀~➁阶段为摆动相，机器人速度为 $v_x$ ，摆动时间为 $T_{swing}$ ，则 $d_{12}=v_x T_{swing}$ 。
➁~➃阶段为支撑相，机器人速度为 $v_x$ ，触底时间为 $T_{stance}$ ，则 $d_{23}=\Delta x=\frac{1}{2} v_x T_{stance}$ 。

图中落脚点 $x_{f}=x_{b}+d_{12}+d_{23}=x_{b}+v_x T_{swing}+\frac{1}{2}v_x T_{stance}$

设相位 $p_{t}=\frac{t-t_{0}}{t_{1}-t_{0}}$ ，则落脚点变为 $x_f=x_{p}(p)+v_x(1-p)T_{swing}+\frac{1}{2}v_xT_{stance}$

若落脚点位于中性落脚点左侧，重力会对落脚点产生顺时针的力矩从而向右加速，所以若 $v_x < v_{xd}$ ，则需左移落脚点。

$\begin{cases} x_{f}=x_{p}(p)+v_{x}(1-p)T_{swing}+\frac{1}{2}v_{x}T_{stance}+k_{x}(v_{x}-v_{xd}) \\ y_{f}=y_{p}(p)+v_{y}(1-p)T_{swing}+\frac12v_{y}T_{stance}+k_{y}(v_{y}-v_{yd}) \end{cases}$

旋转

$\theta_f=\theta_p+\theta_0+\omega(1-p)T_{swing}+\frac{1}{2}\omega T_{stance}+k_\omega(\omega-\omega_d)$

则世界坐标系下的落脚点为

$\begin{cases} x_{f}=R\cos\theta_{f} \\ y_{f}=R\sin\theta_{f} \end{cases}$

结合平移与旋转，落脚点坐标为：

$\begin{cases}x_i=x_b+R\cos\theta_f+v_x(1-p)T_{swing}+\frac{1}{2}v_xT_{stance}+k_x(v_x-v_{xd})\\y_i=y_b+R\sin\theta_f+v_y(1-p)T_{swing}+\frac{1}{2}v_yT_{stance}+k_y(v_y-v_{yd})\end{cases}$

MPC控制器

目标

通过MPC可以得到：

质心位置、速度、加速度、旋转角度、角速度
足底力
足端位置、速度、加速度

让机器狗质心跟踪最新的参考轨迹，计算未来一段时间内的足底力

简化单刚体动力学

下面考虑单刚体动力学：

$\begin{aligned}\ddot{\boldsymbol{p}}=\frac{\sum_{i=1}^n\boldsymbol{f}_i}{m}-\boldsymbol{g}\\\frac{d}{dt}(\boldsymbol{I}\boldsymbol{\omega})=\sum_{i=1}^n\boldsymbol{r}_i\times \boldsymbol{f}_i\end{aligned}$

对上式其进行简化

$\frac{d}{dt}(\boldsymbol{I}\boldsymbol{\omega})=\boldsymbol{I}\boldsymbol{\omega}+\boldsymbol{\omega}\times(\boldsymbol{I}\boldsymbol{\omega})\approx \boldsymbol{I}\dot{\boldsymbol{\omega}}$ ，其中 $\boldsymbol{I}=\boldsymbol{R}\boldsymbol{I}_b\boldsymbol{R}^T\approx \boldsymbol{R}_z(\psi)\boldsymbol{I}_b\boldsymbol{R}_z^T(\psi)$
简化pitch和row

IMU获得的角速度为身体坐标系：
$\begin{aligned} \boldsymbol{\omega}_{s}&=\boldsymbol{R}_{z}(\psi)\boldsymbol{R}_{y}(\theta)\boldsymbol{R}_{x}(\phi)\boldsymbol{\omega}_{b}\\ \boldsymbol{\omega}_{b}&=\left[\boldsymbol{R}_{z}(\psi)\boldsymbol{R}_{y}(\theta)\boldsymbol{R}_{x}(\phi)\right]^{-1}\boldsymbol{\omega}_{s}\\ \left[\begin{matrix}{\dot{\phi}}\\{\dot{\theta}}\\{\dot{\psi}}\\\end{matrix}\right]&=\left[\begin{matrix}{\cos(\psi)/\cos(\theta)}&{\sin(\psi)/\cos(\theta)}&{0}\\{-\sin(\psi)}&{\cos(\psi)}&{0}\\{\cos(\psi)\tan(\theta)}&{\sin(\psi)\tan(\theta)}&{1}\\\end{matrix}\right]\boldsymbol{\omega} \end{aligned}$
在运动过程中机器人的pitch和row均接近于0，故可以忽略
$\begin{aligned} \begin{bmatrix}\dot{\phi}\\\dot{\theta}\\\dot{\psi}\end{bmatrix}&=\begin{bmatrix}\cos(\psi)&\sin(\psi)&0\\-\sin(\psi)&\cos(\psi)&0\\0&0&1\end{bmatrix}\boldsymbol{\omega}\\ &=\boldsymbol{R}_z^T(\psi)\boldsymbol{\omega} \end{aligned}$

状态方程

下面写出状态方程：

状态变量

位置 $\boldsymbol{p}=\begin{bmatrix}x\\y\\z\end{bmatrix}$ ，速度 $\dot{\boldsymbol{p}}=\begin{bmatrix}\dot{x}\\\dot{y}\\\dot{z}\end{bmatrix}$ ，姿态角 $\boldsymbol{\Theta}=\begin{bmatrix}\theta\\\phi\\\psi\end{bmatrix}$ ，姿态角速度 $\boldsymbol{\omega}=\begin{bmatrix}\dot{\theta}\\\dot{\phi}\\\dot{\psi}\end{bmatrix}$ ，重力加速度 $\boldsymbol{g}=\begin{bmatrix}{0}\\{0}\\{-9.8}\\\end{bmatrix}$ 。状态变量则为13维变量： $\boldsymbol{x}=\begin{bmatrix}\boldsymbol{\theta}\\\boldsymbol{p}\\\boldsymbol{w}\\\dot{\boldsymbol{p}}\\g(3)\end{bmatrix}$ 。
控制变量

控制变量为12维变量： $\boldsymbol{u}=\begin{bmatrix}\boldsymbol{f}_1\\\boldsymbol{f}_2\\\boldsymbol{f}_3\\\boldsymbol{f}_4\end{bmatrix}$ 。其中 $\boldsymbol{f}_i$ 为足底力。
状态方程
$\begin{cases}\dot{\boldsymbol{x}}=\boldsymbol{A}\boldsymbol{x}+\boldsymbol{B}\boldsymbol{u}\\\boldsymbol{y}=\boldsymbol{C}\boldsymbol{x}+\boldsymbol{D}\boldsymbol{u}\end{cases}$
将各个已知量带入：
$\frac{d}{dt}\begin{bmatrix}\boldsymbol{\theta}\\\boldsymbol{p}\\\boldsymbol{\omega}\\\dot{\boldsymbol{p}}\\g(3)\end{bmatrix}=\begin{bmatrix} \boldsymbol{0}_{3\times3}&\boldsymbol{0}_{3\times3}&\boldsymbol{R}_{z}^{T}(\psi)&\boldsymbol{0}_{3\times3}&\boldsymbol{0}_{3\times1}\\ \boldsymbol{0}_{3\times3}&\boldsymbol{0}_{3\times3}&\boldsymbol{0}_{3\times3}&\boldsymbol{I}_{3}&\boldsymbol{0}_{3\times1}\\ \boldsymbol{0}_{3\times3}&\boldsymbol{0}_{3\times3}&\boldsymbol{0}_{3\times3}&\boldsymbol{0}_{3\times3}&\boldsymbol{0}_{3\times1}\\ \boldsymbol{0}_{3\times3}&\boldsymbol{0}_{3\times3}&\boldsymbol{0}_{3\times3}&\boldsymbol{0}_{3\times3}&\left[\begin{smallmatrix}0\\0\\1\end{smallmatrix}\right]\\ \boldsymbol{0}_{1\times3}&\boldsymbol{0}_{1\times3}&\boldsymbol{0}_{1\times3}&\boldsymbol{0}_{1\times3}&1\end{bmatrix}\begin{bmatrix}\boldsymbol{\theta}\\\boldsymbol{p}\\\boldsymbol{\omega}\\\dot{\boldsymbol{p}}\\g(3)\end{bmatrix}+ \begin{bmatrix}\boldsymbol{0}_{3\times3}&\boldsymbol{0}_{3\times3}&\boldsymbol{0}_{3\times3}&\boldsymbol{0}_{3\times3}\\\boldsymbol{0}_{3\times3}&\boldsymbol{0}_{3\times3}&\boldsymbol{0}_{3\times3}&\boldsymbol{0}_{3\times3}\\\boldsymbol{I}^{-1}[\boldsymbol{r}_1]_\times&\boldsymbol{I}^{-1}[\boldsymbol{r}_2]_\times&\boldsymbol{I}^{-1}[\boldsymbol{r}_3]_\times&\boldsymbol{I}^{-1}[\boldsymbol{r}_4]_\times\\\boldsymbol{I}_3/m&\boldsymbol{I}_3/m&\boldsymbol{I}_3/m&\boldsymbol{I}_3/m\\\boldsymbol{0}_{1\times3}&\boldsymbol{0}_{1\times3}&\boldsymbol{0}_{1\times3}&\boldsymbol{0}_{1\times3}\end{bmatrix}\begin{bmatrix}\boldsymbol{f}_1\\\boldsymbol{f}_2\\\boldsymbol{f}_3\\\boldsymbol{f}_4\end{bmatrix}$
要想写成代码，需要对其离散化。使用前向欧拉法离散化状态方程：
$\begin{aligned}\dot{\boldsymbol{x}}&=\frac{\boldsymbol{x}_{k+1}-\boldsymbol{x}_k}{\Delta t}=\boldsymbol{A}\boldsymbol{x}_k+\boldsymbol{B}\boldsymbol{u}_k\\\boldsymbol{x}_{k+1}&=\underline{(\boldsymbol{I}+\Delta t\boldsymbol{A})}+\underline{\Delta t\boldsymbol{B}}u_k\\&=\overline{\boldsymbol{A}}\boldsymbol{x}_k+\overline{\boldsymbol{B}}\boldsymbol{u}_k\end{aligned}$
其中的 $\overline{\boldsymbol{A}}$ 和 $\overline{\boldsymbol{B}}$ 表示为：
$\begin{aligned} \overline{\boldsymbol{A}}&=\begin{bmatrix} \boldsymbol{I}_3&\boldsymbol{0}_{3\times3}&\boldsymbol{R}_{z}^{T}(d\psi^k)\Delta T&\boldsymbol{0}_{3\times3}&\boldsymbol{0}_{3\times1}\\ \boldsymbol{0}_{3\times3}&\boldsymbol{I}_3&\boldsymbol{0}_{3\times3}&\boldsymbol{I}_{3}\Delta T&\boldsymbol{0}_{3\times1}\\ \boldsymbol{0}_{3\times3}&\boldsymbol{0}_{3\times3}&\boldsymbol{I}_3&\boldsymbol{0}_{3\times3}&\boldsymbol{0}_{3\times1}\\ \boldsymbol{0}_{3\times3}&\boldsymbol{0}_{3\times3}&\boldsymbol{0}_{3\times3}&\boldsymbol{I}_3&\left[\begin{smallmatrix}0\\0\\1\end{smallmatrix}\right]\Delta T\\ \boldsymbol{0}_{1\times3}&\boldsymbol{0}_{1\times3}&\boldsymbol{0}_{1\times3}&\boldsymbol{0}_{1\times3}&1\end{bmatrix}\\ \overline{\boldsymbol{B}}&=\begin{bmatrix}\boldsymbol{0}_{3\times3}&\boldsymbol{0}_{3\times3}&\boldsymbol{0}_{3\times3}&\boldsymbol{0}_{3\times3}\\\boldsymbol{0}_{3\times3}&\boldsymbol{0}_{3\times3}&\boldsymbol{0}_{3\times3}&\boldsymbol{0}_{3\times3}\\\boldsymbol{I}_k^{-1}[\boldsymbol{r}_1^k]_\times\Delta T&\boldsymbol{I}_k^{-1}[\boldsymbol{r}_2^k]_\times\Delta T&\boldsymbol{I}_k^{-1}[\boldsymbol{r}_3^k]_\times\Delta T&\boldsymbol{I}_k^{-1}[\boldsymbol{r}_4^k]_\times\Delta T\\\boldsymbol{I}_3\Delta T/m&\boldsymbol{I}_3\Delta T/m&\boldsymbol{I}_3\Delta T/m&\boldsymbol{I}_3\Delta T/m\\\boldsymbol{0}_{1\times3}&\boldsymbol{0}_{1\times3}&\boldsymbol{0}_{1\times3}&\boldsymbol{0}_{1\times3}\end{bmatrix} \end{aligned}$

约束

MPC最大的优势就是可以对输入量和状态变量进行约束，所以可以对输入进行约束。输入约束可以分为以下两个约束条件：

足底反力

摆动时足底力为0，state=0， $\boldsymbol{f}_i=\boldsymbol{0}_{3\times1}$

触地时最大足底力为 $f_{max}$ ，state=1， $f_i^z \le f_{max}$
摩擦锥

为保证足底与地面不滑动，足底反力的水平分量不能大于竖直分量 $\times \mu$ ，即
$\begin{aligned}|f_i^x|&\le\mu f_i^z\\|f_i^y|&\le\mu f_i^z\\f_i^z&>0\end{aligned}$

结合以上两个约束，可以得到总的输入约束：

$\begin{bmatrix}0\\0\\0\\0\\0\end{bmatrix}\leq\begin{bmatrix}-1&0&\mu\\0&-1&\mu\\1&0&\mu\\0&1&\mu\\0&0&1\end{bmatrix}\begin{bmatrix}{f_i}^x\\{f_i}^y\\{f_i}^z\end{bmatrix}\leq\begin{bmatrix}+\infty\\+\infty\\+\infty\\+\infty\\f_{\max}\end{bmatrix}$

优化问题

首先建立代价函数（式中 $Q$ 、 $R$ 为对角正定/半正定矩阵，需要对其进行调参）

$\min_{x,u}\sum_{i=0}^{K-1}\underset{误差加权和}{\underline{\|x_{i+1}-x_{i+i,ref}\|Q_{i}}}+\underset{输入加权和}{\underline{\|u_{i}\|R_{i}}}$

使其满足：

$\begin{cases}x_{i+1}=A_{i}x_{i}+B_{i}u_{i}&,i=0\cdots k-1\\\underline{c_{i}}\leq C_iu_i\leq\overline{c_{i}}&,i=0\cdots k-1(\text{支撑相})\\D_{i}u_{i}=0&,i=0\cdots k-1(\text{摆动相})&\end{cases}$

对其进行二次规划，化为qpOASES标准形式：

$\boxed{ \begin{aligned} \min_{x}\quad&\frac12x^THx+x^Tg(w_0)\\s.t.\quad&lbA(\omega_0)\leq Ax\leq ubA(\omega_0)\\&lb(\omega_0)\leq x\leq ub(\omega_0) \end{aligned} }$

预测步长为 $n$ ，状态量 $X_k=\begin{bmatrix}x_k^{k+1}\\x_k^{k+2}\\\vdots\\x_k^{k+n}\end{bmatrix}$ ，输入量 $U_{k}=\begin{bmatrix}u_{k}^{k}\\u_{k}^{k+1}\\\vdots\\u_{k}^{k+n-1}\end{bmatrix}$ ，则

$X_{k}=\begin{bmatrix}\overline{A}\\\overline{A}^{2}\\\vdots\\\overline{A}^{N}\end{bmatrix}x_{k}+\begin{bmatrix}\overline{B}&0&\cdots&0\\\overline{A}\overline{B}&\overline{B}&\cdots&\vdots\\\vdots&\vdots&\ddots&\vdots\\\overline{A}^{N-1}\overline{B}&\overline{A}^{N-2}\overline{B}&\cdots&\overline{B}\end{bmatrix}U_{k}$

上式可以记为 $X=A_{qp}x_0+B_{qp}U$ 。对于目标值 $X^{\mathrm{ref}}=\begin{bmatrix}x^{k+1}\\x^{k+2}\\\vdots\\x^{k+n}\end{bmatrix}$ ，优化问题可以转化为：

$\begin{aligned} \min_U\quad J(U)&=\| X-X^{\mathrm{ref}}\| L+\| U\| K\\ &=(X-X^{ref})^{T}L(X-X^{ref})+U^{T}KU\\ &=(A_{qp}x_0+B_{qp}U-y)^T L(A_{qp}x_0+B_{qp}U-y)+U^TKU\\ &=(x_0^TA^T_{qp}+U^TB_{qp}^T-y^T)L(A_{qp}x_0+B_{qp}U-y)+U^TkU\\ &=U^T(B^T_{qp}LB_{qp}+K)U+U^TB_{qp}^TL(A_{qp}x_0-y)+(A_{qp}x_0-y)^TLB_{qp}U+(A_{qp}x_0-y)^TL(A_{qp}x_0-y)\\ &=U^T(B_{qp}^TLB_{qp}+K)U+U^TB_{qp}^TL(A_{qp}x_0-y)+[U^TB_{qp}^TL(A_{qp}x_0-y)]^T+(A_{qp}x_0-y)^TL(A_{qp}x_0-y) \end{aligned}$

观察上式，第二第三项L左右均为向量且L为对角阵，故两者相同；第四项中的 $A_{qp}x_0-y$ 无控制量的影响，仅为状态量的变化，为常数项，可以省略。故上式可以整理为：

$\begin{aligned} \min_U\quad J(U) &=U^T(B_{qp}^TLB_{qp}+K)U+2U^TB_{qp}^TL(A_{qp}x_0-y) \end{aligned}$

即可以整理为：

$\begin{aligned} \min_U \quad& \frac12U^THU+U^Tg\\ s.t. \quad& \underline{c}\leq CU\leq\overline{c}\end{aligned}$

其中：（维度中的 $n$ 为足数4， $k$ 为单次MPC的迭代次数）

$\begin{aligned} H&=2(B_{qp}^TLB_{qp}+K)\in\mathbb{R}^{3nk\times3nk}\\ g&=2B_{qp}^TL(A_{qp}x_{0}-y)\in\mathbb{R}^{3nk\times1}\\ \end{aligned}$

至此可得机器狗跟踪质心轨迹的一组最优足端支撑力， $u_0=\begin{bmatrix}f_1\\f_2\\f_3\\f_4\end{bmatrix}$

WBC控制器

计算关节位置、速度、加速度

零空间

通过MPC可得到最优足端力 $\boldsymbol{u}_0$ ，可通过 $\boldsymbol{\tau}=\boldsymbol{J}(\boldsymbol{\theta})^T\boldsymbol{F}$ 计算关节力矩，但只适用于低速场景。在高速场景下，足端与地面的接触时间非常短，无法进行优化，此时动态性能较差，故需要使用WBC控制器，其输入参数为接触状态、支撑力、足端轨迹、质心轨迹。且其控制频率比MPC快。

当机器人高速运动时，四条腿触地时间很短，机器人大部分时间处于欠驱动状态，与无人机欠驱动系统不同，四足机器人与地面的频繁接触变成了干扰项。此时机器人相当于与一个虚拟浮动基座相连。此虚拟浮动基座有6个自由度（冗余），此时机器人的状态变得不确定。

将需要控制的变量进行优先级划分，使用零空间理论：

级别	内容	约束
0级	足端接触力	高级别
1级	机器人姿态	不能翻
2级	机器人位置	可适量浮动
3级	摆动退轨迹	低级别

冗余自由度机器人的优化

$\boldsymbol{A}$ 的零空间是 $\boldsymbol{A}\boldsymbol{x}=\boldsymbol{0}$ 的所有解 $\boldsymbol{x}$ 的集合，也就是 $\boldsymbol{x}$ 固定，无论 $\boldsymbol{A}$ 取何值，结果均为0。类比串联机械臂，末端固定而其他关节转动时，所有能转动的位形构成零空间。

前文推导了末端速度与关节角速度之间的关系：$\dot{\boldsymbol{x}}=\boldsymbol{J}(\boldsymbol{\theta})\dot{\boldsymbol{\theta}}$ ，若 $\boldsymbol{J}(\boldsymbol{\theta})$ 可逆，可以得到 $\dot{\boldsymbol{\theta}}=\boldsymbol{J}^{-1}(\boldsymbol{\theta})\dot{\boldsymbol{x}}$ 。

若对于机械臂，遇到奇异位形，或关节数大于末端坐标数，此时 $\boldsymbol{J}(\boldsymbol{\theta})$ 不可逆。故引入伪逆， $\boldsymbol{J}(\boldsymbol{\theta})$ 的伪逆表示为 $\boldsymbol{J}^{\dagger}(\boldsymbol{\theta})$ ，无论 $\boldsymbol{J}(\boldsymbol{\theta})$ 是否可逆，关节角速度均可表示为 $\dot{\boldsymbol{\theta}}=\boldsymbol{J}^{\dagger}(\boldsymbol{\theta})\dot{\boldsymbol{x}}$ 。

伪逆的计算可以分两种情况

欠约束，关节数n＜末端坐标数m， $\boldsymbol{J}^{\dagger}\boldsymbol{J}=\boldsymbol{I},\boldsymbol{J}^{\dagger}=(\boldsymbol{J}^{T}\boldsymbol{J})^{-1}$ ，此时方程可能无解，用代价函数使结果逼近设定值。
冗余约束，关节数n＞末端坐标数m， $\boldsymbol{J}\boldsymbol{J}^{\dagger}=\boldsymbol{I},\boldsymbol{J}^{\dagger}=\boldsymbol{J}^T(\boldsymbol{J}\boldsymbol{J}^{T})^{-1}$ ，此时方程有无数解，设定关节约束得到最优结果。

对于冗余约束机械臂，若想在保持末端位姿不变的前提下控制其他关节的状态，则需利用零空间。

$\dot{\boldsymbol{\theta}}=\boldsymbol{J}^{\dagger}(\boldsymbol{\theta})\dot{\boldsymbol{x}}$ 是一个特解，其通解为 $\dot{\boldsymbol{\theta}}=\boldsymbol{J}^{\dagger}(\boldsymbol{\theta})\dot{\boldsymbol{x}}+(\boldsymbol{I-}\boldsymbol{J}^{\dagger}(\boldsymbol{\theta})\boldsymbol{J}(\boldsymbol{\theta}))\boldsymbol{z}$ TODO原理

将 $\dot{\boldsymbol{x}}$ 称为任务空间， $\dot{\boldsymbol{\theta}}$ 称为控制空间， $\boldsymbol{z}$ 称为零空间。 $\dot{\boldsymbol{x}}$ 中为高优先级的任务， $\boldsymbol{z}$ 中为低优先级的任务。

两个任务

对于两个任务，高优先级任务为 $\dot{\boldsymbol{w}}_1$ ，低优先级任务为 $\dot{\boldsymbol{w}}_2$

$\begin{aligned} \dot{\boldsymbol{w}}_{1}=\boldsymbol{J}_1(\boldsymbol{\theta})\dot{\boldsymbol{\theta}}\\ \dot{\boldsymbol{w}}_{2}=\boldsymbol{J}_{2}(\boldsymbol{\theta})\dot{\boldsymbol{\theta}}\\ \end{aligned}$

对于第一个高优先级任务的式子，其冗余控制方程为：

$\dot{\boldsymbol{\theta}}=\boldsymbol{J}_{1}^{\dagger}(\boldsymbol{\theta})\dot{\boldsymbol{w}}_{1}+(\boldsymbol{I}-\boldsymbol{J}_{1}^{\dagger}(\boldsymbol{\theta})\boldsymbol{J}_{1}(\boldsymbol{\theta}))\boldsymbol{z}$

将其带入第二个式子，得到：

$\dot{\boldsymbol{w}}_{2}=\boldsymbol{J}_{2}(\boldsymbol{\theta})(\boldsymbol{J}_{1}^{\dagger}(\boldsymbol{\theta})\dot{\boldsymbol{w}}_{1}+(\boldsymbol{I}-\boldsymbol{J}_{1}^{\dagger}(\boldsymbol{\theta})\boldsymbol{J}_{1}(\boldsymbol{\theta}))\boldsymbol{z})$

整理得：

$\boldsymbol{J}_{2}(\boldsymbol{\theta})(\boldsymbol{I}-\boldsymbol{J}_{1}^{\dagger}(\boldsymbol{\theta})\boldsymbol{J}_{1}(\boldsymbol{\theta}))\boldsymbol{z}=\dot{\boldsymbol{w}}_{2}-\boldsymbol{J}_{2}(\boldsymbol{\theta})\boldsymbol{J}_{1}^{\dagger}(\boldsymbol{\theta})\dot{\boldsymbol{w}}_1$

此时结果可能不唯一，使用最小二乘法优化代价函数。同样需要分为以下两种情况：

欠约束， $\min |\boldsymbol{z}|_2$
冗余约束， $\min |\boldsymbol{J}_{2}(\boldsymbol{\theta})(\boldsymbol{I}-\boldsymbol{J}_{1}^{\dagger}(\boldsymbol{\theta})\boldsymbol{J}_{1}(\boldsymbol{\theta}))\boldsymbol{z}-\dot{\boldsymbol{w}}_{2}+\boldsymbol{J}_{2}(\boldsymbol{\theta})\boldsymbol{J}_{1}^{\dagger}(\boldsymbol{\theta})\dot{\boldsymbol{w}}_1|_2$

多个任务

推广到一般形式，对于n个任务，符合任务优先级的关节速度为：

$\begin{aligned}\dot{\boldsymbol{q}}&=\sum_{i=1}^{n}\boldsymbol{N}_{i}\dot{\boldsymbol{q}}_{i}\\ \dot{\boldsymbol{q}}_{i}&=(\boldsymbol{J}_{i}\overline{\boldsymbol{N}_{i}})^{\dagger}(\dot{\boldsymbol{x}}_{i}^{*}-\boldsymbol{J}_{i}\sum_{n=1}^{n-1}\boldsymbol{N}_{k}\dot{\boldsymbol{q}}_{k})\end{aligned}$

式中 $\dot{\boldsymbol{x}}_{i}^{*}$ 为最优解， $\overline{\boldsymbol{N}_{i}}$ 为组合雅可比矩阵 $\overline{\boldsymbol{J}_{i}}$ 的零空间投影矩阵， $\overline{\boldsymbol{J}_i}=\begin{bmatrix}\boldsymbol{J}_1\\\boldsymbol{J}_2\\\vdots\\\boldsymbol{J}_{i-1}\end{bmatrix}$ 为所有任务优先级高于 $i$ 的任务的雅可比矩阵的组合。

写成迭代形式：

$\dot{\boldsymbol{q}}_{i}=\dot{\boldsymbol{q}}_{i-1}+(\boldsymbol{J}_{i}\boldsymbol{N}_{i-1})^{\dagger}(\dot{\boldsymbol{x}}_{i}^{*}-\boldsymbol{J}_{i}\dot{\boldsymbol{q}}_{i-1})$

关节位置

根据上文的推导，可以得到关节位置的迭代形式：

$\begin{aligned} \Delta\boldsymbol{q}_{1} &=\boldsymbol{J}_1^\dagger(\boldsymbol{x}_1^{des}-\boldsymbol{x}_1)\\ \Delta\boldsymbol{q}_{2} &=\Delta\boldsymbol{q}_1+\boldsymbol{J}_{2|pre}^\dagger(\boldsymbol{x}_2^\mathrm{des}-\boldsymbol{x}_2-\boldsymbol{J}_2\Delta\boldsymbol{q}_1)\\ &\vdots \\ \Delta\boldsymbol{q}_{i} &=\Delta\boldsymbol{q}_{i-1}+\boldsymbol{J}_{i|pre}^{\dagger}(\boldsymbol{x}_{i}^{\mathrm{des}}-\boldsymbol{x}_{i}-\boldsymbol{J}_{i}\Delta\boldsymbol{q}_{i-1}) \end{aligned}$

其中：

$\begin{aligned} &\boldsymbol{J}_{i|pre}=\boldsymbol{J}_{i}\boldsymbol{N}_{i-1}, \\ &\boldsymbol{N}_{i-1}=\boldsymbol{N}_{0}\boldsymbol{N}_{1|0}\cdots\boldsymbol{N}_{i-1|i-2}, \\ &\boldsymbol{N}_{0}=\boldsymbol{I}-\boldsymbol{J}_{c}^{\dagger}\boldsymbol{J}_{c}, \\ &\boldsymbol{N}_{i|i-1}=\boldsymbol{I}-\boldsymbol{J}_{i|i-1}{}^{\dagger}\boldsymbol{J}_{i|i-1}. \end{aligned}$

其中 $\boldsymbol{J}_i$ 为第 $i$ 项任务雅可比矩阵； $\boldsymbol{x}_{i}^{\mathrm{des}}$ 为第 $i$ 项任务的期望位置； $\Delta\boldsymbol{q}_{i}$ 为根据第 $i$ 项任务迭代计算出的关节位置增量； $\boldsymbol{J}_{i|pre}$ 为第 $i$ 项任务到先前任务的零空间投影； $\boldsymbol{J}_c$ 为接触约束雅可比矩阵；

关节速度与加速度

同理可以得到关节速度与加速度（ $\text{dyn}$ 代表动态一致伪逆： $\overline{\boldsymbol{J}^{\mathrm{dyn}}}=\boldsymbol{A}^{-1}\boldsymbol{J}^T\left(\boldsymbol{J}\boldsymbol{A}^{-1}\boldsymbol{J}^T\right)^{-1}$ ）：

$\begin{aligned}\dot{\boldsymbol{q}}_i^{\mathrm{cmd}}&=\dot{\boldsymbol{q}}_{i-1}^{\mathrm{cmd}}+\boldsymbol{J}_{i|pre}^{\dagger}\left(\dot{\boldsymbol{x}}_i^{\mathrm{des}}-\boldsymbol{J}_i\dot{\boldsymbol{q}}_{i-1}^{\mathrm{cmd}}\right),\\\ddot{\boldsymbol{q}}_i^{\mathrm{cmd}}&=\ddot{\boldsymbol{q}}_{i-1}^{\mathrm{cmd}}+\overline{\boldsymbol{J}_{i|pre}^{\mathrm{dyn}}}\left(\ddot{\boldsymbol{x}}_i^{\mathrm{cmd}}-\dot{\boldsymbol{J}}_i\dot{\boldsymbol{q}}-\boldsymbol{J}_i\ddot{\boldsymbol{q}}_{i-1}^{\mathrm{cmd}}\right)\end{aligned}$

其中（ $\boldsymbol{K}_p$ 和 $\boldsymbol{K}_d$ 分别是位置和速度反馈增益，cmd代表控制命令）：

$\begin{aligned} \boldsymbol{q}_i^{\mathrm{cmd}}&=\boldsymbol{q}_i+\Delta\boldsymbol{q}_i\\ \ddot{\boldsymbol{x}}_i^\mathrm{cmd}&=\ddot{\boldsymbol{x}}^\mathrm{des}+\boldsymbol{K}_p\left(\boldsymbol{x}_i^\mathrm{des}-\boldsymbol{x}_i\right)+\boldsymbol{K}_d\left(\dot{\boldsymbol{x}}^\mathrm{des}-\dot{\boldsymbol{x}}\right) \end{aligned}$

计算出的 $\boldsymbol{q}_i^{\mathrm{cmd}}$ 和 $\dot{\boldsymbol{q}}_i^{\mathrm{cmd}}$ 发送到关节PD控制器、 $\ddot{\boldsymbol{q}}_i^{\mathrm{cmd}}$ 发送到QP规划器计算扭矩命令

计算关节力矩

浮动基动力学模型

对于固定机械臂这种基坐标系固定的机器人，只需知道每个关节的角度即可知道机器人的姿态。但对于四足机器人来说基座是不固定的，故需要在世界系与浮动基座机器人本体系之间建立一个没有实体的 6 自由度关节，其关节空间向量为 $\boldsymbol{q}={\begin{bmatrix}\boldsymbol{q}_f\\\boldsymbol{q}_j\end{bmatrix}}$ ，其中 $\boldsymbol{q}_f$ 代表身体浮动基的6个自由度， $\boldsymbol{q}_j$ 代表关节的12个自由度。浮动基动力学方程为：

$\boldsymbol{A}\ddot{\boldsymbol{q}}+\boldsymbol{b}+\boldsymbol{g}=\boldsymbol{S}_j^T\boldsymbol{\tau}+\boldsymbol{J}_{int}^T\boldsymbol{f}_{int}-\boldsymbol{J}_c^T\boldsymbol{f}_i$

上式中 $\boldsymbol{A}$ 为质量（惯量）矩阵； $\boldsymbol{b}$ 为可科氏力与离心力项； $\boldsymbol{g}$ 为重力项； $\boldsymbol{S}_j$ 为驱动关节选择矩阵，将驱动关节的扭矩映射到整个配置空间； $\boldsymbol{f}_{int}$ 为内力； $\boldsymbol{f}_i$ 为足底力； $\boldsymbol{J}$ 为约束雅可比矩阵，其中 $int$ 代表内部约束； $c$ 代表接触约束， $\boldsymbol{J}$ 满足下式：

$\begin{aligned} \boldsymbol{0}&=\boldsymbol{J}\dot{\boldsymbol{q}} \\\boldsymbol{0}&=\boldsymbol{J}\ddot{\boldsymbol{q}}+\dot{\boldsymbol{J}}\dot{\boldsymbol{q}} \end{aligned}$

松弛优化

在机器人的运动过程中需要遵循动力学方程以及满足一些不等式约束来保证机器人的稳定，故使用QP优化。引入松弛变量 $\boldsymbol{\delta}_{f_{r}}$ 、 $\boldsymbol{\delta}_{f}$ ，允许机器人基座与期望状态之间存在偏差，这使得机械狗在一些不可控制的姿态条件下，仍能计算出相应的控制信号，更有利于机器人的高速运动。

$\begin{aligned} \mathrm{min} \quad& \boldsymbol{\delta}_{f_r}^T\boldsymbol{Q}_1\boldsymbol{\delta}_{f_r}+\boldsymbol{\delta}_f^T\boldsymbol{Q}_2\boldsymbol{\delta}_f\\ \mathrm{s.t} \quad& \boldsymbol{S}_f (\boldsymbol{A}\ddot{\boldsymbol{q}}+\boldsymbol{b}+\boldsymbol{g})=\boldsymbol{S}_f \boldsymbol{J}_c^T\boldsymbol{f}_r\quad&\text{(浮动基动力学方程)}\\ &\ddot{\boldsymbol{q}}=\ddot{\boldsymbol{q}}^{\mathrm{cmd}}+\begin{bmatrix}\boldsymbol{\delta}_f\\\boldsymbol{o}_{nj}\end{bmatrix}\quad&\text{(加速度)}\\ &\boldsymbol{f}_r=\boldsymbol{f}_r^{\mathrm{MPC}}+\boldsymbol{\delta}_{f_r}\quad&\text{(足端接触反力)}\\ &\boldsymbol{W}\boldsymbol{f}_{r}\geq \boldsymbol{0} \quad&\text{(足端摩擦约束)} \end{aligned}$

其中， $\boldsymbol{f}_r^{\mathrm{MPC}}$ 为MPC计算的支撑腿的反作用力； $\boldsymbol{S}_f$ 为选择矩阵； $\boldsymbol{W}$ 为权重矩阵；

将优化出的地面反力、关节加速度及前文计算得到的关节位置、速度带到动力学方程里，可以求出支撑腿、摆动腿的关节力矩（对于摆动腿来说 $\boldsymbol{f}_r=0$ ）：

$\begin{bmatrix}\boldsymbol{\tau}_f\\\boldsymbol{\tau}_j\end{bmatrix}=\boldsymbol{A}\ddot{\boldsymbol{q}}+\boldsymbol{b}+\boldsymbol{g}-\boldsymbol{J}_c\boldsymbol{f}_r$

向电机发送控制力矩

之后使用求得的关节力矩做为前馈，再加上关节位置、速度的PD控制，对机器人的支撑腿、摆动腿进行控制。

$\boldsymbol{\tau}_{i}=\boldsymbol{\tau}^\mathrm{cmd}+\boldsymbol{K}_{p}\left(\boldsymbol{q}_{i}^\mathrm{cmd}-\boldsymbol{q}_{i}\right)+\boldsymbol{K}_{d}\left(\dot{\boldsymbol{q}}_{i}^\mathrm{cmd}-\dot{\boldsymbol{q}}_{i}\right)$